【高校数I】三角比の相互関係の公式を証明する【苦手克服】

ジル

みなさんおはこんばんにちは。

大掃除するのがめちゃくちゃめんどくさいジルでございます！

みなさん数Iの三角比について、次の公式を多用しているかと思います。

$\sin \theta =\cos \theta \tan \theta$

${\sin }^2\theta +{\cos }^2\theta =1$

$1+{\tan }^2\theta =\frac{1}{{\cos }^2\theta }$

今回は少し箸休めということで、こちらを証明してみます。

ジル

別に興味のない方は見なくても大丈夫です笑

公式がなかなか覚えられない方は一度証明を見ると頭に入るかもですね！

まずは

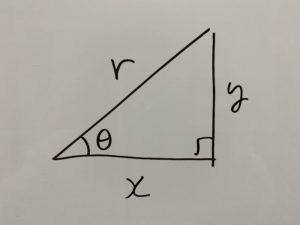
一般的な直角三角形のこちらを利用します。この時

$\sin \theta =\frac{y}{r}$

$\cos \theta =\frac{x}{r}$

$\tan \theta =\frac{y}{x}$

であることは以前の記事で解説しましたね？

【高校数I】三角比の基本のキを元数学科が解説する【苦手克服】

今記事は、【高校数学】【数I】『図形と数量』の三角比の初めの基礎を解説しました。図も交えながら分かりやすい解説を心がけましたのでよかったらご覧ください。

www.zilleblog.com

2020.12.17

$\sin \theta =\cos \theta \tan \theta$の証明

$(\mathrm{右}\mathrm{辺})=\frac{x}{r}\times \frac{y}{x}=\frac{y}{r}=\sin \theta$

これだけです。

${\sin }^2\theta +{\cos }^2\theta =1$の証明

$(\mathrm{左}\mathrm{辺})=(\frac{y}{r}{)}^2+(\frac{x}{r}{)}^2=\frac{y^2}{r^2}+\frac{x^2}{r^2}=\frac{x^2+y^2}{r^2}$

ここで中学数学で学んだ『三平方の定理』を思い出してもらいたいです。

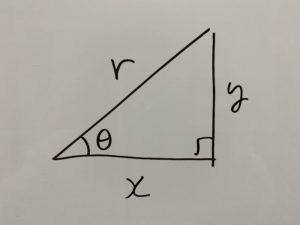
上のような三角形がある時、

$x^2+y^2=r^2$

が成立します。これを先程の計算過程に代入すると

$(\mathrm{左}\mathrm{辺})=\frac{x^2+y^2}{r^2}=\frac{r^2}{r^2}=1$

$１+{\tan }^2\theta =\frac{1}{{\cos }^2\theta }$の証明

$(\mathrm{左}\mathrm{辺})=1+(\frac{y}{x}{)}^2=1+\frac{y^2}{x^2}=\frac{x^2}{x^2}+\frac{y^2}{x^2}=\frac{x^2+y^2}{x^2}$

ここで三平方の定理より

$(\mathrm{左}\mathrm{辺})=\frac{x^2+y^2}{x^2}=\frac{r^2}{x^2}=(\frac{r}{x}{)}^2=(\frac{1}{\frac{x}{r}}{)}^2=(\frac{1}{\cos \theta }{)}^2=\frac{1}{{\cos }^2\theta }$

最後に

今回は簡単ではありますが公式の解説をしてみました！

証明を見て公式を正しく理解すればより知識が身につくでしょう。

ジル

楽しい数学Lifeを！

DJCD「イヤホンズの三平方の定理」 [ 高野麻里佳／高橋李依／長久友紀 ]

楽天ブックス

Amazon

楽天