【高校数I】三角比の拡張の公式を証明する【苦手克服】

ここ最近私はこのブログで『三角比』についての記事を投稿しております。

その中で次の公式を紹介しました。

 

$\sin (90°-θ)=\cos θ$

$\cos (90°-θ)=\sin θ$

$\tan (90°-θ)=\frac{1}{\tan θ}$

 

$\sin (180°-θ)=\sin θ$

$\cos (180°-θ)=-\cos θ$

$\tan (180°-θ)=-\tan θ$

 

今回はなんでこうなるのか解説してみたいと思います！

 

$９０°-θ$の各場合を解説

次の三角形を使って解説します。

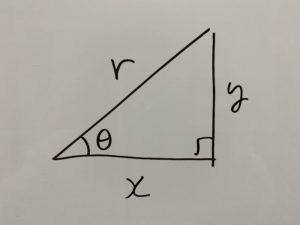
注目すべきは

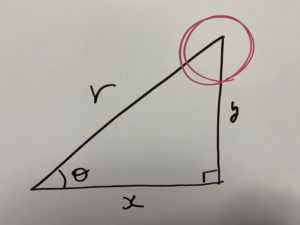
ここの角度なんですね！三角形の内角の合計が180°であるため

$180°-θ-90°=90°-θ$

つまり

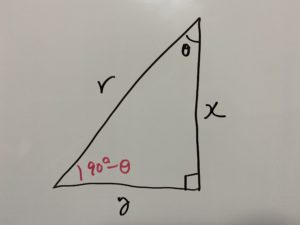
こうやって三角形を回転させれば$\sin (90°-θ)$、$\cos (90°-θ)$、そして$\tan (90°-θ)$を求められます。

 

$\sin (90°-θ)=\frac{x}{r}$

$\cos (90°-θ)=\frac{y}{r}$

$\tan (90°-θ)=\frac{x}{y}$

さてここで図１をもう一度見てみましょう。

$\sin θ=\frac{y}{r}$

$\cos θ=\frac{x}{r}$

$\tan θ=\frac{y}{x}$

 

 

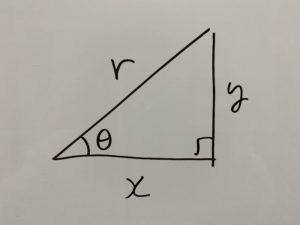
気づきましたか？

$\sin (90°-θ)=\frac{x}{r}=\cos θ$

$\cos (90°-θ)=\frac{y}{r}=\sin θ$

$\tan (90°-θ)=\frac{x}{y}=\frac{1}{\frac{y}{x}}=\tan θ$

になっているんですね！

 

 

$１８０°-θ$の各場合を解説

ここでは半径を１とする『単位円』を使うと分かりやすいです。

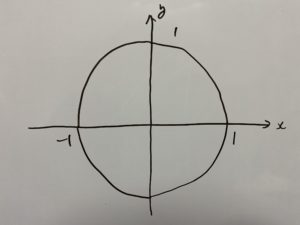
今回は$0° \leqq θ \leqq 180°$なので上の半円のみ扱います。

 

 

この時単位円上の点についてこう置きます。

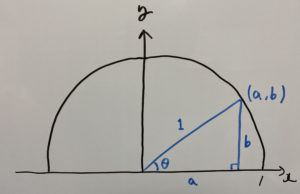
ここで青色の三角形のsin θ、cos θ、tan θを求めます。

$\sin θ=\frac{b}{1}=b$

$\cos θ=\frac{a}{1}=a$

$\tan θ=\frac{b}{a}$

つまりですね、こう表せるようになります。

 

 

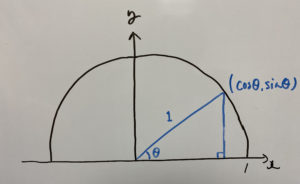
こうなるんですよ！これを言葉で定義すると

『単位円と0°から傾きθの直線との交点のx座標が$\cos θ$、y座標が$\sin θ$』

 

 

ここで$180°-θ$の場合を考えます。先程赤線で引いた定義を利用すると

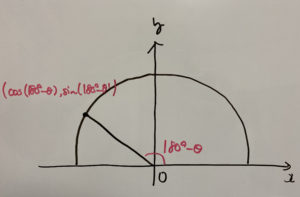
こうなりますね。

ここで次の部分にできる三角形に注目しましょう。

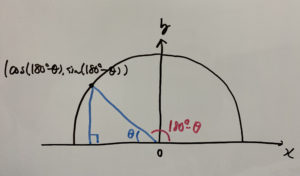
この時、x軸において、180°から傾きがθだけ時計回りに出ているため先程の単位円上の三角形と見比べると分かりやすいのですが

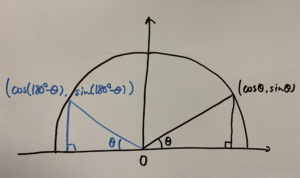
この２つの三角形って合同なんですよね。

 

なのでどっちの点もy座標は$\sin θ$なんですよね実は。

またこの半円はy軸について左右対象ですので、x座標は$-\cos θ$になります。

 

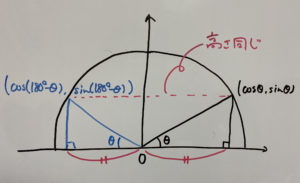
したがって

$\sin (180°-θ)=\sin θ$

$\cos (180°-θ)=-\cos θ$

$\tan (180°-θ)=\frac{\sin (180°-θ)}{\cos (180°-θ)}=\frac{\sin θ}{-\cos θ}=-\tan θ$

 

 

最後に

解説は理解できましたか？

図もたくさん交えながら頑張って解説しました！褒めて！w

次回は問題編の記事を書こうかと考えています。