
みなさんおはこんばんにちは。
最近太ってきて焦っているジルでございます!
今回は「三角形の内分」「三角形の外分」「三角形の内心」「三角形の外心」「三角形の重心」について解説します。
みなさんは図形の問題は得意ですか?
図形の問題で重要なのは
「情報をしっかり漏らすことなく図に書き込むこと」
です。
これを疎かにすると情報に漏れが出てしまいます。
もちろん数学ができる人は必要な情報のみ厳選できることでしょう。苦手な方は「どれが問題を解くのに必要なのか?」なんて考えなくてもいいのでとにかく得られる情報は全て書き出しましょう。問題をこなすうちに段々と情報の取捨選択ができるようになります。
さて、今回のテーマと少しずれてしまいましたが、ここらで話題を戻しまして解説していきたいと思います。
三角形の比(内分・外分)
まずはある三角形△ABCを用意します。
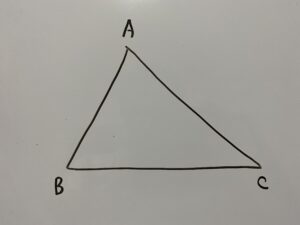
内分
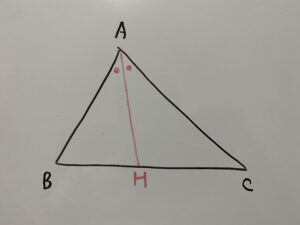
この時次が成立します。
証明
この証明をするには2本の平行線両方に交わる直線について、角に関する次の定理を知っておく必要があります。
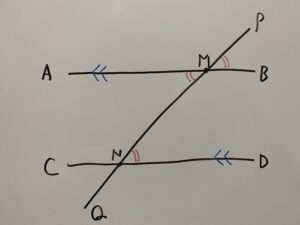
が成立する。

こちらは中学生の時習った内容ですね。
忘れてたという方は今すぐ頭に叩き込みましょう٩( ‘ω’ )و
後もう一つ
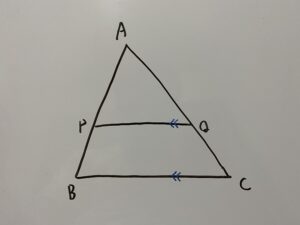
が成立する。
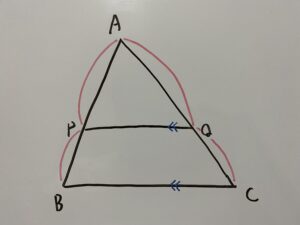
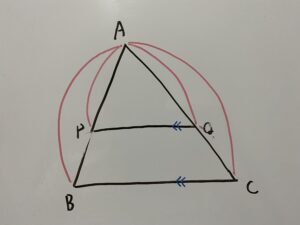

上の2つが成立するならば当然
も成立します!
では本編に入ります。
先程の△ABCを用意しまして、
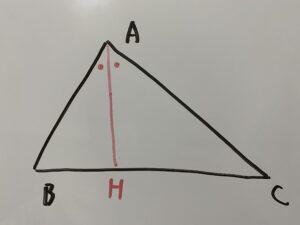
ここで、頂点Bを通りAHと平行な線を書き、ACを延長した線との交点をDとおく。
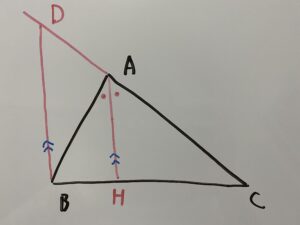
辺AHは
①、②を③に代入すると
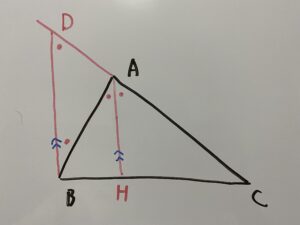
△ACDついて、④より
図を少し回転させましょう。
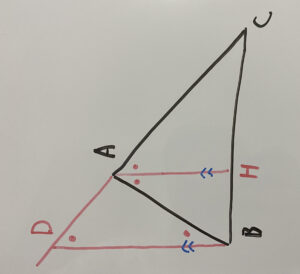
この時、
外分
△ABCを用意します。
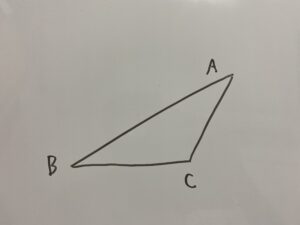
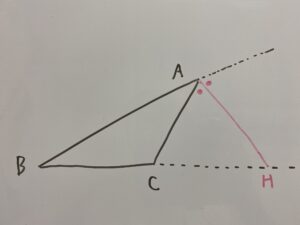
この時

内分と比べると少しイメージしづらい公式かもですね…。
証明
またABの延長線上にGを定義して、頂点Cを通ってAHに平行な直線とABとの交点をDとおく。
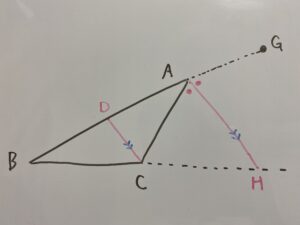
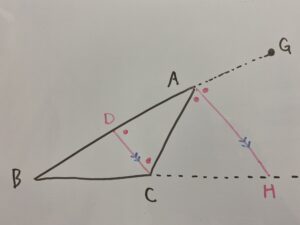
△ADCについて、
△ABHについて、
三角形の内心・外心・重心
内分、外分を学んだ後は『内心・外心・重心』について勉強しましょう。

それぞれ少し似ていますが、間違えないようにしましょう!
『三角形の内心』とは、三角形の3つの角の2等分線が交わる点です。
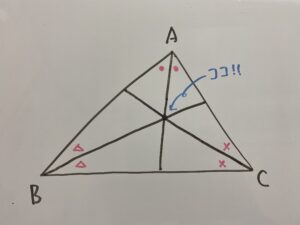
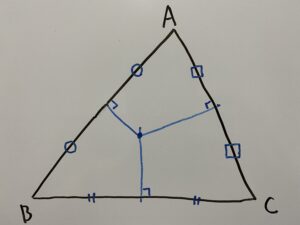
『三角形の外心』とは、3辺の垂直二等分線が交わる点です。
図に書くと
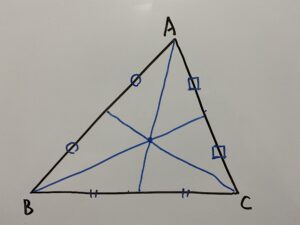
『三角形の重心』とは、三角形の各頂点から対辺へ描く中線が交わる点です。
図に書くと
ここでみなさん、なぜ内心、外心と呼ぶか分かりますか?
それは内心の場合、
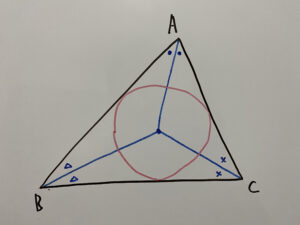
このように、内心と内接円の中心が同じだからです。
外心の場合も、
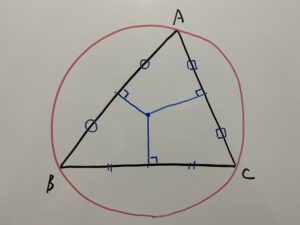
外心と外接円の中心が同じだからです。

なんか円ズレてね…?

そこは気にしてはいけない。
重心の特徴は
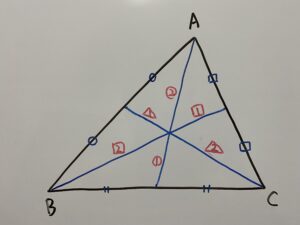
のように各中線を2:1に内分していることです。
練習問題
「内分」「外分」「内心」「外心」「重心」について学びましたので、せっかくですから練習問題を解いてみましょう!
問①
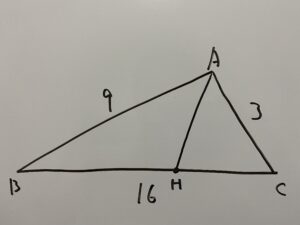
この時BH、CHの長さを求めなさい。

内分に関する基本問題です。これが解けなくては話にならないので確実に解けるようにしましょう。
《解答》
です。
AB=9、AC=3より代入して
ここで
ここで三角形を見てみましょう。
ここに
つまり
答えは
問②
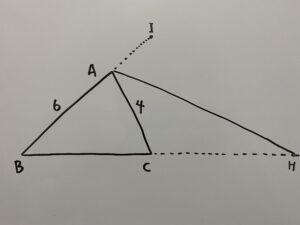
この時BC、HCの長さを求めなさい。

外分に関する基本問題です。問①と同様に確実に解けるようになりましょう!
《解答》
図より点Hは△ABCの頂点Aに関する外分点であることがわかります。
よって
です。(外分の説明はこちら)
図よりBH=16なので代入して
答えは
問③
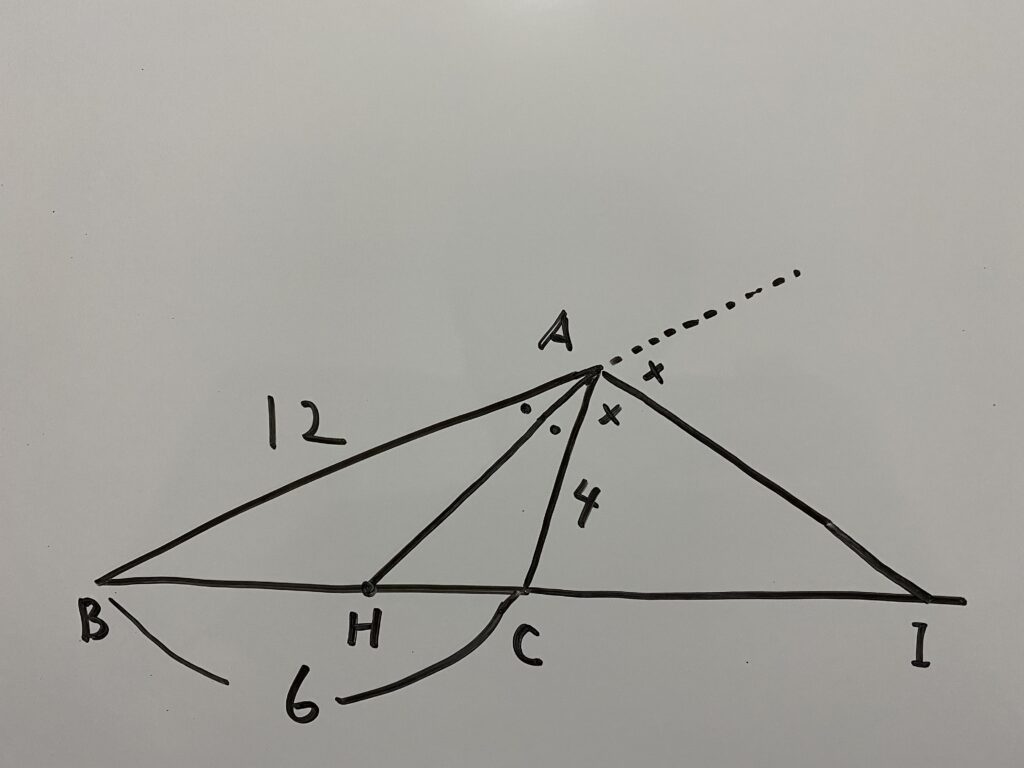
この時次の長さを求めなさい。
(1)BH(2)CH(3)BI

内分と外分の混合問題です。
《解答》
(1)
BHについて、点Hは△ABCの頂点Aに対する内分点であるので
AB=12、AC=4なので代入すると
つまり
ここで図をもう一度見ていただくと、
先程の
答えは
(2)
これは(1)ででましたね?答えは
(3)
図を見ると、点Iは△ABCについて、頂点Aに対する外分点です。
つまり
答えは
問④
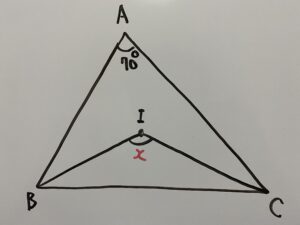
点Iは△ABCの内心である。この時xの角度を求めなさい。

こういうパターンの問題ではまず線を付け足すのが大切です。
《解答》
まずは『内心』の復習から

内分の性質より
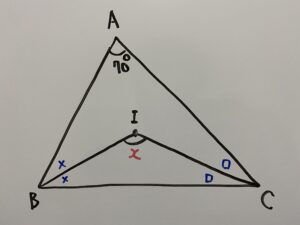
三角形の各頂点の内角の合計は180°ですから
次に△IBCを見てみましょう。
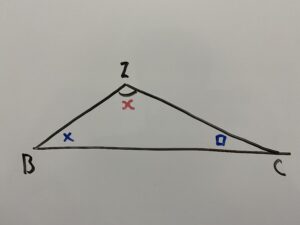
三角形の内角を全て足すと180°ですから
①を代入して
答えは125°
まとめ

この時次が成立します。
頂点Aから図のような外分線を引く。BCの延長戦との交点をHとおく。

この時




なにやら難しそうな定理ですが、頑張ってわかりやすい記事を書きますので期待していてください(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

楽しい数学Lifeを!

あ、言われちった…。



