みなさんおはこんばんにちは、GWが終わり悲壮感に打ちひしがれているジルでございます！
今回は『三平方の定理』を『空間図形の問題』に応用して問題を解いてみたいと思います。
問題を解くコツ
まず問題を解くコツをお伝えします。
①ゴールを見据えて、そのために明らかにすべきところを逆算する。
これができると楽です。
できるかどうかは練習量がものをいいます。
なんどもなんども口を酸っぱくして行っていますが、数学上達の一番の近道はとにかく問題を解く事！努力は裏切りません。
たくさんの問題を解くと似た問題に出会う確率がその分上がりますよね？すると「あ、これ解いたことあるな。確かこうやって…」ってなる訳です。
・ただし鍛錬が必要
・たくさん問題を解いて練習しよう！
ただしこれはできる人の場合。できない人は②の方法でいきましょう。
②分かるところをひたすら書き出して、攻略の糸口を見つける。
泥臭い方法ですがこれが現実的でしょうね。
時間がかかるし、別に必要ないところまで求めることになりますが、確実です！
・しかし確実に解ける。
・②で経験を積んで、①で解けるように頑張ろう！！！
実際に問題を解いてみよう！
問１
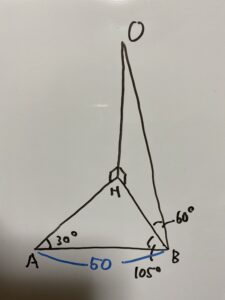
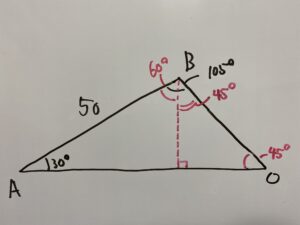
次のような図形を考えます。この時OHの長さを求めなさい。
____________________________________________________________________________________
解説のあとに答えを書いてあります。
「先に答えが見たいよ！」って方はこちらから飛べますので！
解説
先程の「①ゴールを見据えて、そのために明らかにすべきところを逆算する。」をもとに解いてみましょう。
まずはOHを含む△OHBを見てみます。
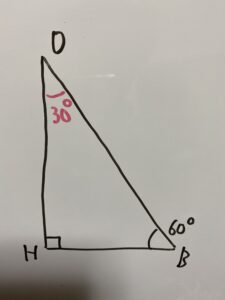
ここで分かっている情報を全て書き出すのが大切です。
ここである程度問題をこなしている方はこう考えるはずです。
あれ？これ三平方の定理の応用
『30°,60°,90°』
のパターン使えるのでは？
ということはBHかOBがわかれば答え（OH）が導き出せる訳です。
ここでどちらを求めるか問題が出てきますよね？これもある程度やっている方はすぐに見当つきます。
OBは△ABOにも含まれている…ということはこちらの方が導き出しやすいのでは？
それ正解！
ということで次は△ABOに注目してみましょう。
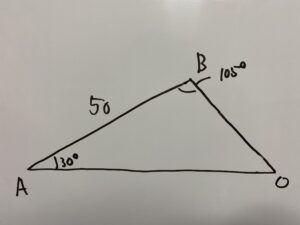
ここでしっかり現在分かっている情報を書き込みこと！
さてこの三角形を見ると私はすぐに１本線を引きたくなります。
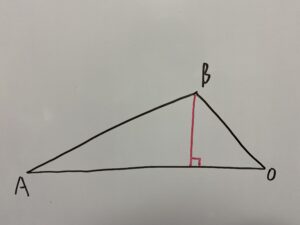
すると一気に正解に近づく訳です。なぜなら
「30°,60°,90°を持つ三角形」と「45°,45°,90°を持つ三角形」ができあがるからです！
ーーーーー《復習》ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
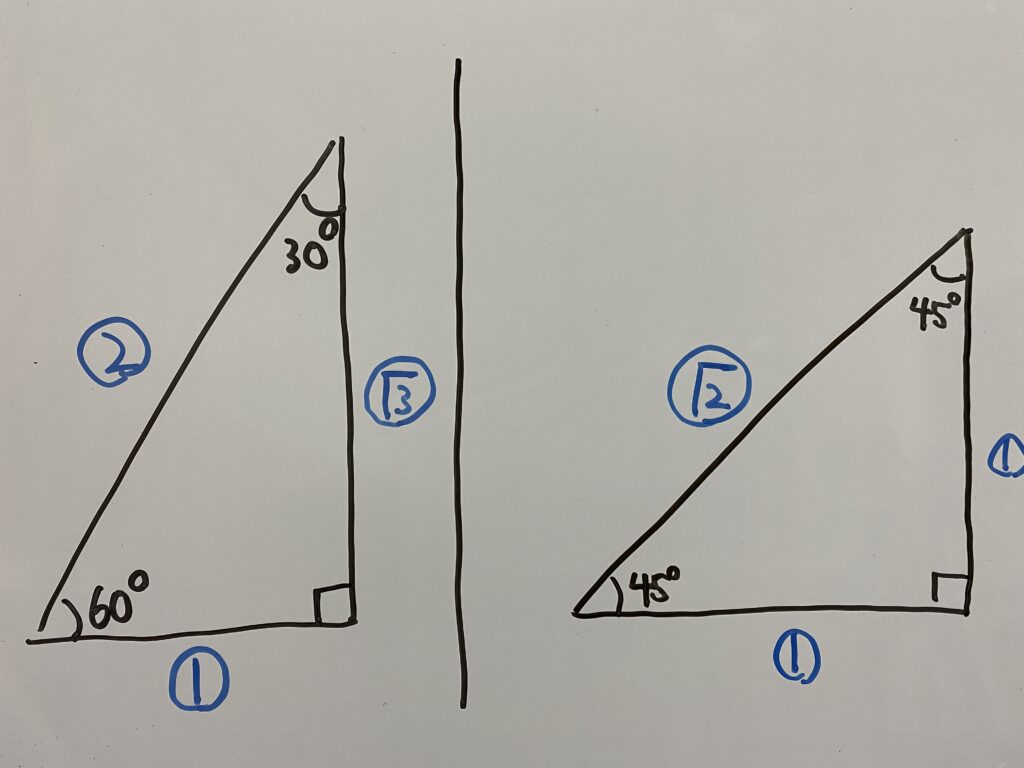
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
現在分かっている辺はAB=50のみ。
ですが三平方の定理を使えば全ての辺の長さが分かっちゃいます！
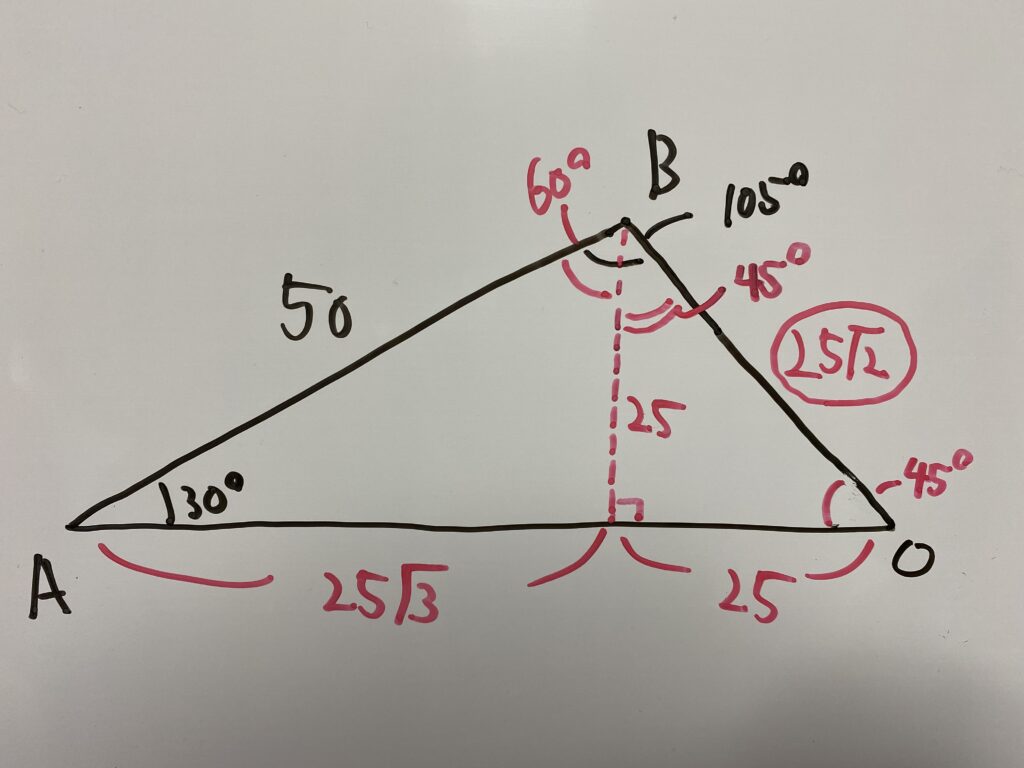
今回はOBを求めたかったのでOB=25√2
あとは
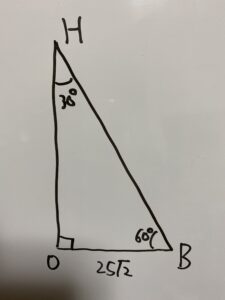
の三角形について三平方の定理「30°,60°,90°の三角形」を使って
$OH=25\sqrt{6}$
解答例
△ABOについて考える。
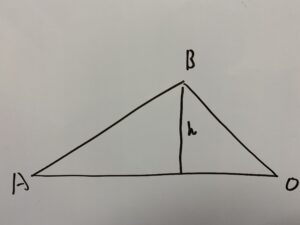
図のような線を書き足し、その長さをhと定義する。
hについて三平方の定理より
$2:1=50:h$
$h=25$
次にOBについて三平方の定理より
$1:\sqrt{2}=25:OB$
$OB=25\sqrt{2}$
次に△OBHについて考える。
OHについて三平方の定理より
$1:\sqrt{3}=25\sqrt{2}:OH$
$OH=25\sqrt{6}$ 以上
問２
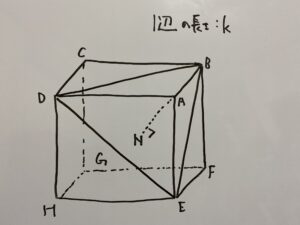
次のような立方体を考える。辺の長さをkとする。
また頂点Aから△BDEで引いた垂線の足をNとする。
この時次の問いに答えなさい。
（１）△BDEの面積をSとして、Sを求めなさい。
（２）三角錐A-BDEの体積をVとして、Vを求めなさい。
（３）ANの長さを求めなさい。
____________________________________________________________________________________
この問題の答えも解説の後に載せてあります！
さっさと見たい方はこちらから飛んでね（＾∇＾）
（１）「△BDEの面積をSとして、Sを求めなさい。」の解説
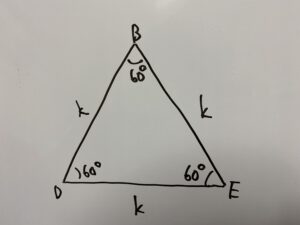
△BDEについての問題になりますので、まずは△BDEを書いてみましょう。
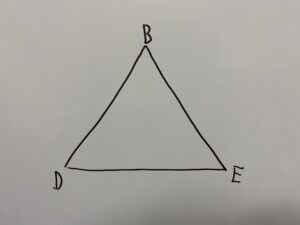
なんにも情報がない…だと( ﾟдﾟ)
少しづつ情報を集めましょう！
まずこの三角形が「正三角形」であることは分かりますか？
全ての辺が
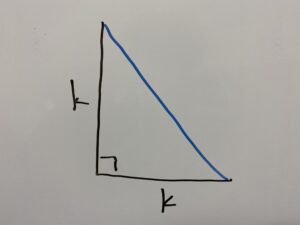
つまり三平方の定理『45°,45°,90°』を使えば
$1:\sqrt{2}=k:○$
$○=\sqrt{2}k$
ここから本題の面積を求めてみます。
方法は次の３つです。
②$S=\frac{1}{2}bc\sin A$を使って解く。
③ヘロンの公式を使って解く。
以前この辺りを詳しくまとめた記事を書いたのでご覧あれ(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
どの方法を使えばいいのかなぁ？？
どの方法でもいいです。私は公式を覚えていないので①を使います。
解説では全ての方法を試してみますね！
①正弦定理・余弦定理を使って解く。
これなんですが、今回は角度が出ているのでかなーり省いて解けます。
まずは線を引きまして、底辺との交点をHと置きましょう。
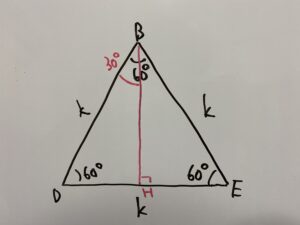
△BDHについて、三平方の定理『30°,60°,90°』を使って
$2:\sqrt{3}=\sqrt{2}k:BH$
$2BH=\sqrt{6}k$
$BH=\frac{\sqrt{6}}{2}$
したがって、1/2 x （底辺） x（高さ）より
$\frac{1}{2} \times \sqrt{2}k \times \frac{\sqrt{6}}{2}$
$=\frac{12}{4}k^2=\frac{2\sqrt{3}}{4}k^2=\frac{\sqrt{3}}{2}k^2$
②$S=\frac{1}{2}bc\sin A$を使って解く。
早速掛けます。
$\frac{1}{2} \times \sqrt{2}k \times \sqrt{2}k \times \sin 60°$
$\frac{1}{2} \times \sqrt{2}k \times \sqrt{2}k \times \frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}}{2}k^2$
③ヘロンの公式を使って解く。
$s=\frac{a+b+c}{2}$と置くと
$S=\sqrt{s(s-a)(s-b)(s-c)}$
これ考えた人すごいよなぁ
$s=\frac{\sqrt{2}k+\sqrt{2}k+\sqrt{2}k}{2}=\frac{3\sqrt{2}k}{2}$
$S=\sqrt{\frac{3\sqrt{2}}{2}k(\frac{3\sqrt{2}}{2}k-\sqrt{2}k)^3}$
$=\sqrt{\frac{3\sqrt{2}}{2}k(\frac{\sqrt{2}}{2}k)^3}=\sqrt{\frac{3\sqrt{2}}{2}k(\frac{2\sqrt{2}}{8})k^3}$
$=\sqrt{\frac{3\sqrt{2}}{2}k(\frac{\sqrt{2}}{4})k^3}=\sqrt{\frac{6}{8}k^4}$
$=\sqrt{\frac{3}{4}k^4}=\frac{\sqrt{3}}{2}k^2$
（２）「三角錐A-BDEの体積をVとして、Vを求めなさい。」の解説
まずは体積の求め方を復習しましょう。
〇〇柱⇨$（底面積）\times（高さ）$
〇〇錐⇨$（底面積）\times（高さ）\times \frac{1}{3}$
こちらは結構長い解説です。
恐縮ですが、数学が苦手な方でも理解できる記事を目指しておりますのでご了承くださいm(__)m
一般的な参考書の解説以上の丁寧さを心がけております。
ちなみにこの解き方よりも早い解き方があります。
さっさと見たい方はこちらから飛べますので。
まずは図形を書き出しますと
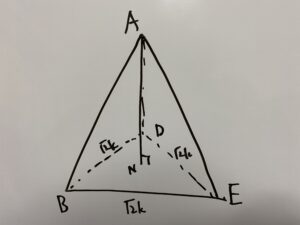
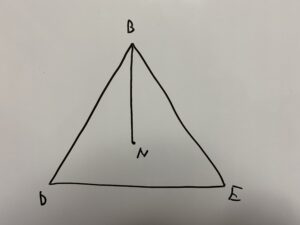
これは感覚的に分かります。
詳しく説明すると逆にややこしくなるので
・AB=AD=AEなのでAから降りてくる垂線ANはBN=DN=ENとなる訳です。
次に先程の画像に、分かっている情報を少し書き加えます。
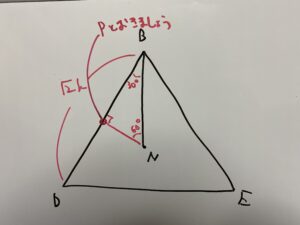
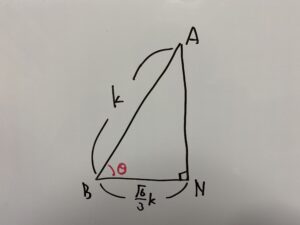
やっと三角錐A-BDEの底面積・高さが明らかになりました(ﾟ∀ﾟ)
あとは〇〇錐の公式
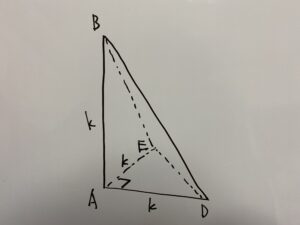
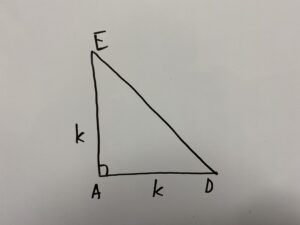
（３）「ANの長さを求めなさい。」の解説
こちらの問題、実は
で考えている場合（２）で求めています笑
なので
で（２）を解いていた場合の解説をしますね。
解答例
三平方の定理より
$1:\sqrt{2}=k:DE$
$DE=\sqrt{2}k$
BD,BEも同様に$\sqrt{2}k$。よって△BDEは正三角形。
次の図のように頂点Bから辺DEへ垂線を引き、次のようにHを定義する。
三平方の定理より
$2:\sqrt{3}=\sqrt{2}:BH$
$2BH=\sqrt{6}k$
$BH=\frac{\sqrt{6}}{2}$
したがって△BDEの面積は
$\frac{1}{2} \times \sqrt{2}k \times \frac{\sqrt{6}}{2}k=\frac{\sqrt{12}}{4}k^2=\frac{\sqrt{3}}{2}k^2$
（２）三角錐B-ADEを考える。
△ADEの面積を考える。
$\frac{1}{2} \times k \times k=\frac{1}{2}k^2$
したがって三角錐B-ADEの体積は
$\frac{1}{2}k^2 \times k \times \frac{1}{3}=\frac{1}{6}k^3$
三角錐A-BDEと三角錐B-ADEの体積は等しいため、$\frac{1}{6}k^3$
（３）三角錐A-BDEを考える。
底面である△BDEの面積は（１）で求めており、体積は（２）で求めたため
$\frac{\sqrt{3}}{2}k^2 \times AN times \frac{1}{3}=\frac{1}{6}k^3$
$\frac{\sqrt{3}}{6}k^2 an=\frac{1}{6}k^3$
$\sqrt{3}AN=k$
$AN=\frac{k}{\sqrt{3}}=\frac{\sqrt{3}}{3}k$
最後に
今回の記事はなかなか超大作になりましたね笑
じっくり解説を書いていたらいつのまにかこんなになっていました。
次は『データの分析』の分野を解説したいと思っています。
楽しい数学Lifeを！
