
みなさんこんにちは、ジルでございます!
今回は高校数学数Iで学ぶ『因数分解』にて必須になる「たすきがけ」を解説したいと思います!
すでにたすきがけをマスターしている方は本記事は見なくても大丈夫かと思います。
そもそも『たすきがけ』とはなんぞや?
先日、因数分解の基礎について書いた記事を公開しました。

その中で、因数分解の一般式
acx²+(ad+bc)x+bd=(ax+b)(cx+d) a,b,c,dは定数
のお話をしました。この中のa,b,c,dを求める方法が「たすきがけ」です。
まず、たすきがけのやり方を図を使って表してみます。
因数分解の一般式
acx²+(ad+bc)x+bd=(ax+b)(cx+d) a,b,c,dは定数
について
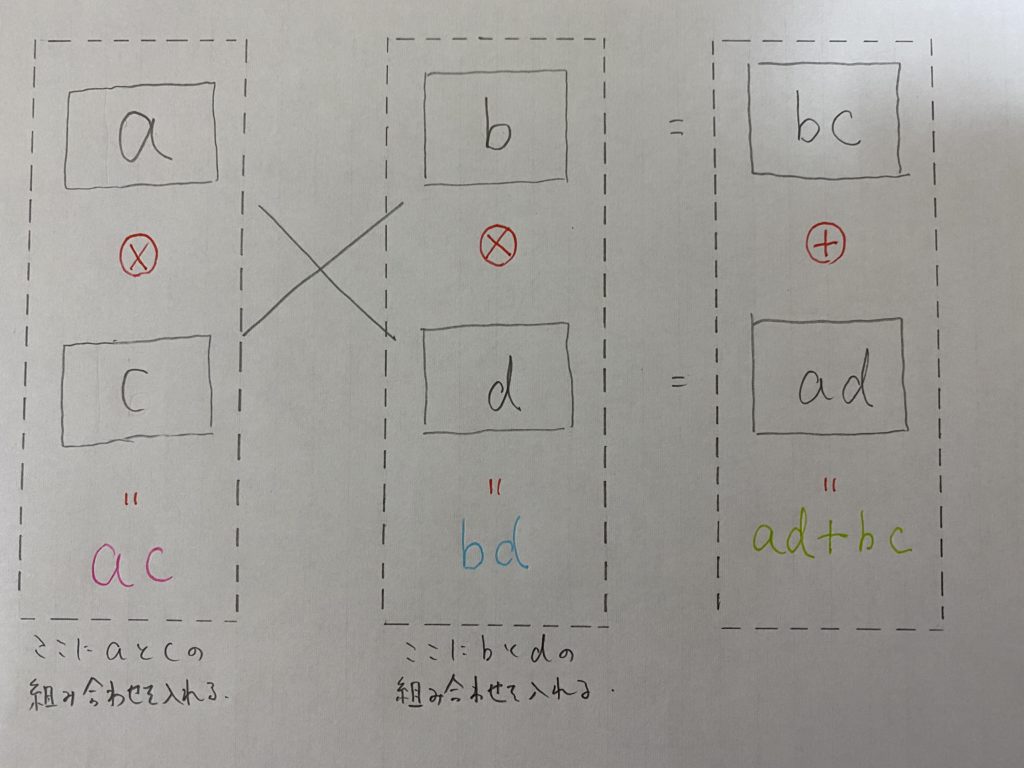
のような図を用いて解きます。
解く順序は
❷ bdの組み合わせを考える。
❸ ad+bcが問題に一致するようにa,b,c,dを調整する。

これをマスターすれば複雑な因数分解も解けるようになります。
始めはかなり苦労しますが、数をこなせば楽になっていきますよ!
実際に問題をやってみよう
実際にたすきがけを使って問題を解いてみましょう。
とその前に、因数分解の解き方の確認をします。
①問題をじっくり眺める。
②共通項があれば、ab+ac=a(b+c)のようにしてまとめる。
③a²+2ab+b²=(a+b)²
a²−b²=(a+b)(a−b)
の公式が使えるかチェックする。使えれば使って、使えなければ④へ。
④acx²+(ad+bc)+bd=(ax+b)(cx+d) a,b,c,dは定数
を使って解く。
こちらも確認しながらやっていきましょう。
ちなみに、たすきがけは④で使うものです。③までに解けるなら解いてしまいましょう。
問1 4x²+4x−15
①問題をじっくり眺める。
じっくり眺めましょう。問題をたくさん解けばこの段階で「あ、こうやって解くと良さそう
やな。」と分かってきます。
②共通項があれば、ab+ac=a(b+c)のようにしてまとめる。
今回は共通項はなさそうです。
③a²+2ab+b²=(a+b)²
a²−b²=(a+b)(a−b)
の公式が使えるかチェックする。使えれば使って、使えなければ④へ。
2つの公式はどちらも使えなさそうです。
④acx²+(ad+bc)+bd=(ax+b)(cx+d) a,b,c,dは定数
を使って解く。
今回の問題は頭でパッと因数分解はできなさそうです。

ではたすきがけを使いましょう。
まずは④の公式と今回の問題を見比べてみましょう。
acx²+(ad+bc)x+bd=(ax+b)(cx+d)
4x²+4x-15
つまり、
ac=4 ad+bc=4 bd=-15 になるようなabcdを求めれば良い!
では先ほど示した順序に従って求めていきましょう。
❶acの組み合わせを考える。
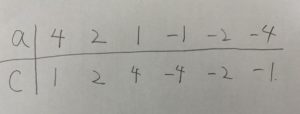
ここで1つアドバイス。
ac>0の時はa<0かつc<0の場合は考えなくてもいいです。
分かっている方はいいですが、一応押さえておきますね。よって
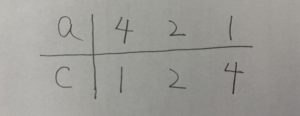
❷bdの組み合わせを考える。
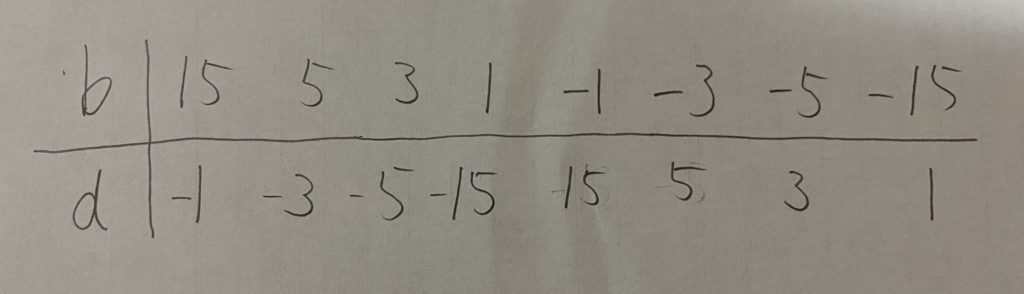
❸ad+bcが問題に一致するようにabcdを調整する。
さあもう終盤です。先ほど教えた
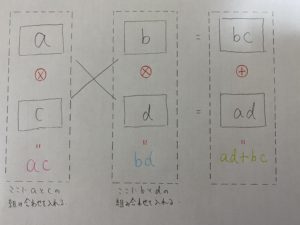
に代入してきましょう。
今回はad+bc=4になる組み合わせを探します。
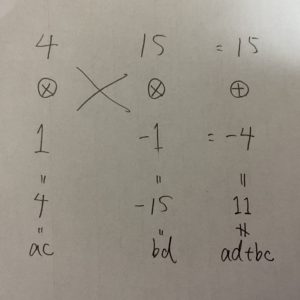
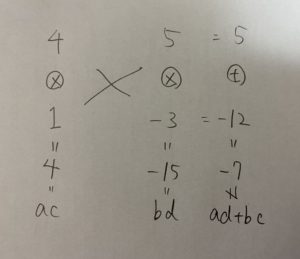
こうやって各組み合わせを試していくと
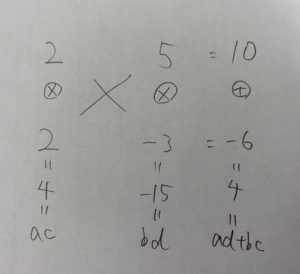
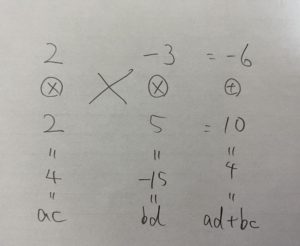
この時、ad+bc=4になりますね!
つまり
4x²+4x−15=(2x+5)(2x−3) または 4x²+4x−15=(2x-3)(2x+5)
ということです。
ここでみなさん気づきますか?上の2つの答えって同じですよね?
なのでとちらか好きな方を書けばOKです。 終わり!
答えについて少し補足
今回は全ての組み合わせを試してもらいました。
すると今回のように答えが複数出てくることがあります。
しかしその場合、結局同じです(カッコの順番が違うだけだったり、マイナスのついている位置が違うだけだったり)。
つまり何が言いたいのかというと、
❸にて各組み合わせを試していく中で、ad+bcが一致したら残りの組み合わせは試す必要がない
ということです。
もちろん全部試した方が間違いは減りますが、解答に時間がかかってしまい、他の問題に割く時間がなくなってしまうのはやはり良くないです。

いっぱい問題をこなしましょう。やればやるほどたすきがけのスピード・精度が向上します。努力は裏切りません。
最後に
たすきがけは最初はかなり時間がかかるし大変です。
どうやったら早く解けるようになるか?それは「いっぱい問題を解く」これに尽きます。
教科書や問題集の問題をひたすら解きましょう。
今回解いた問題は1つだけでしたが、別記事で数問解き方をお見せしたいと思います。記事が書け次第、下にリンクを貼るのでよかったらご覧ください。

繰り返しになりますが努力は裏切りません!頑張りましょう。





