【高校数学】正弦定理・余弦定理を利用して三角形の面積を求める。

早速ですがみなさん、三角形の面積の求め方はご存知でしょうか？

 

ずばり

$\frac{1}{2} \times (底辺) \times (高さ)$

ですね？

 

これはみなさん知っていることでしょう( ^ω^ )

しかし毎回毎回丁寧に底辺・高さが記載されている問題ばかりではありません。

 

今回は高さが書いていない三角形の面積を正弦定理・余弦定理を使って求めていこうと思います！

 

 

練習問題

次のような三角形を使います。

 

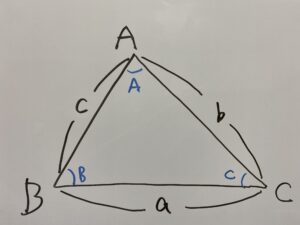
この時次の条件を満たす三角形の面積Sを求めなさい。

 

 

問題①

 

$b=5,c=2\sqrt{3},A=60°$

 

一度図に起こしてみましょう。

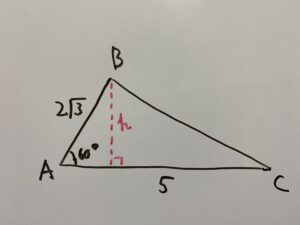
この場合は図のような『高さ』を直接求めることができます。

 

三平方の定理より次の三角形の各辺は次の比率になります。

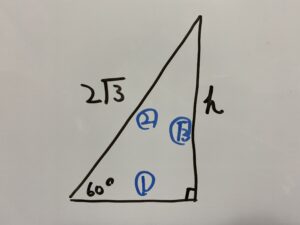
高さをhとすると

$2:\sqrt{3}=2\sqrt{3}:h$

$2h=6$

$h=3$

 

したがって面積Sは

$S=\frac{1}{2} \times 5 \times 3=\frac{15}{2}$

 

 

問題②

 

$a=8,b=6,c=4$

 

一度図に起こしてみましょう。

 

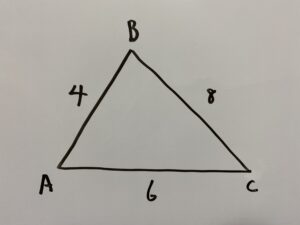
さてまずは先程の問題のように解けるかやってみましょう。

まずは$\angle A$を出してみます。

 

余弦定理より

$8^2=6^2+4^2-2 \times 6 \times 4 \times\cos A$

⇩（式変形）

$64=36+16-48\cos A$

⇩（式変形）

$48\cos A=-12$

⇩（式変形）

$\cos A=-\frac{1}{4}$

 

ここで問題発生

Aの角度がわかりません！！！

 

 

ここで注目して欲しいのは

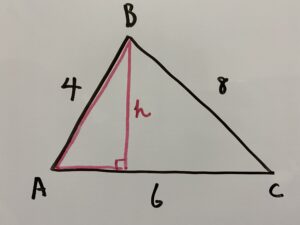
この三角形に注目します。sinAは

$\sin A=\frac{h}{AB}$

AB=4なのであとはsinAが分かればhも分かるということです！

 

先ほどcosAを出しました。なので$\sin^2 A+\cos^2 A=1$を利用すればいけます。

 

$\sin^2 A+(-\frac{1}{4})^2=1$

⇩（式変形）

$\sin^2 A=1-\frac{1}{16}=\frac{15}{16}$

⇩（式変形）

$\sin A=\frac{\sqrt{15}}{4}$

$0° \lt A \lt 180°$なので$A \gt 0$なため。

 

これを先程の$\sin A=\frac{h}{AB}$に代入して

 

$\frac{\sqrt{15}}{4}=\frac{h}{4}$

⇩（式変形）

$h=\sqrt{15}$

 

したがって面積Sは

$S=\frac{1}{2} \times 6 \times \sqrt{15}$

 

 

公式

 

さてここまで解いてきましたが実はまとめた公式が存在します。

 

上記の三角形においてその面積をSとすると

$S=\frac{1}{2}bc\sin A$、$\frac{1}{2}ca\sin B$、$\frac{1}{2}ab\sin C$

 

もちろん公式を使って解くのも良いです。しかし覚えていなくとも解けるんだと言うのも知っておいて欲しいです。

 

最後に

正弦定理・余弦定理を実践的に使う例を紹介しました。

次はもう少し難しめの応用問題を解いてみようと思います。