
みなさんおはこんばんにちは。
身体中が筋肉痛なジルでございます!
今回から数Aを学んでいきましょう。
まずは『場合の数と確率』からです。

まずはどこから手ぇつけるんや??

最初は『集合』です。
まだ何も勉強していないと「集合ってなんぞや?」となることでしょう。
まずは概念を整理。
数学における集合とは、大雑把に言えばいくつかの「もの」からなる「集まり」である。
- 「集合」『フリー百科事典 ウィキペディア日本語版』。2021年5月20日 (木) 13:12 UTC、URL: https://ja.wikipedia.org
基本の確認

必須単語について
次にこの分野を学ぶ上で欠かせない語句を覚えましょう。
○
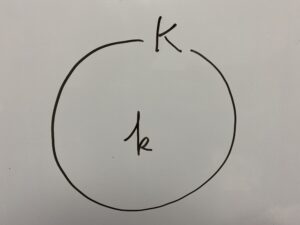
○
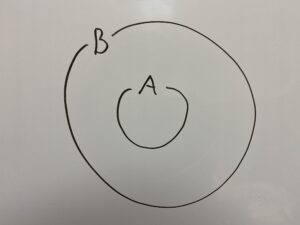
○
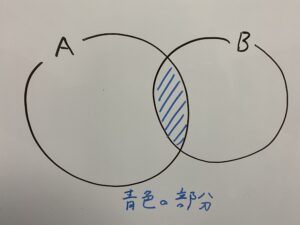
○
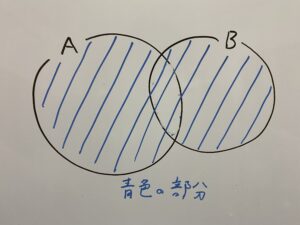
○
○
補集合ともいう。
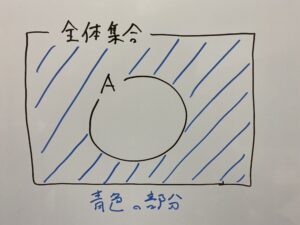
「ベン図」について
先ほどの説明でよく使っていた画像は集合を図にしたものでベン図といいます。

これからよく使っていきますので( ^ω^ )
集合の「個数」について
集合Aについて、その要素の個数が有限である時、その個数をn(A)と表す。
練習問題

各単語の意味を求めるため、練習問題を解いていきましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
問
次の集合を定義します。
全体集合U={1,2,3,4,5,6,7,8,9}
A={1,3,5,6,8}
B={2,3,6,9}
この時
を求めなさい。
《解答》

とりあえずベン図を描いてみましょう。
これができたら楽勝っすわ!
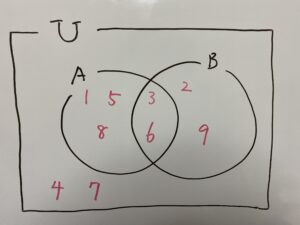
こちらの部分です。
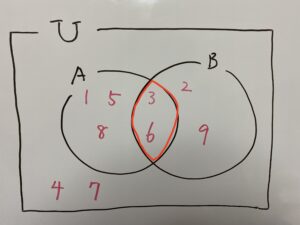
したがって
こちらの部分です。
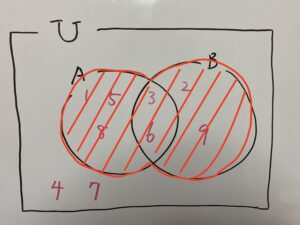
したがって
こちらの部分です。
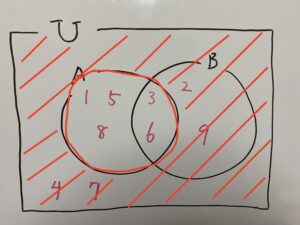
したがって
こちらの部分です。
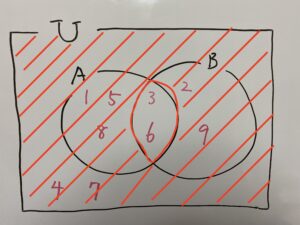
したがって
A={1,3,5,6}ということで要素は4つ

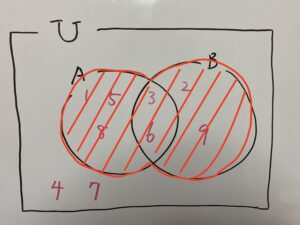
まとめ
○
○
○
○
○
補集合ともいう。

私もできるだけ分かりやすい記事を書き続けますので一緒に頑張りましょう!
楽しい数学Lifeを!


![高校数学I:集合・命題・証明【電子書籍】[ 大西一弘 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/1781/2000004401781.jpg?_ex=128x128)

