みなさんおはこんばんにちは。
最近加湿器を使いだしたジルでございます！
今回は二次不等式の応用問題を解説します。
基礎、基本問題の記事も書いてありますので、基礎に不安のある方はご覧ください。
ではいきます。
次の二次不等式を満たす整数$x$を求めなさい。
まずはこちら。ポイントなのは『整数』ということです。
$２x^2+3x-9 \leqq 0$
まずはこの二次方程式についての情報を集めましょう。
・$x^2$の係数は2のため、これは下に凸。
・左辺の判別式は、$D=3^2-4 \times 2 \times (-9)=9+72=81 \gt 0$。よって$x$軸との交点は２つ。
・$2x^2+3x-9=0$を解くと、
$x=\frac{-3\pm\sqrt{3^2-4 \times 2 \times (-9)}}{2 \times 2}=\frac{-3\pm\sqrt{81}}{4}=\frac{-3\pm9}{4}$
したがって$x=\frac{3}{2},-3$
これらをまとめると次のようなグラフになります。
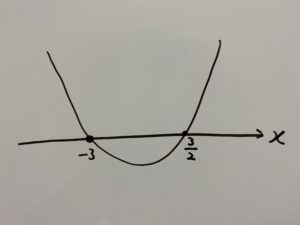
今回はあくまで”整数”なので
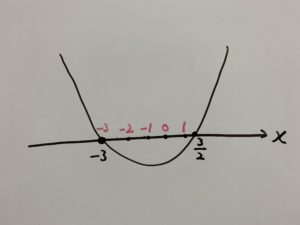
つまり$x=-3,-2,-1,0,1$
$x^2-4x+3 \lt 0$
さて情報収集しよっか！
・$x^2$の係数は1のためこの二次不等式は下に凸。
・左辺の判別式$D=(-4)^2-4 \times 1 \times 3=4 \gt 0$。つまり$x$軸との交点は２つ。
・$x^2-4x+3=0$を解くと、$(x-3)(x-1)=0$つまり$x=1,3$。
これらをまとめると次のようなグラフになります。
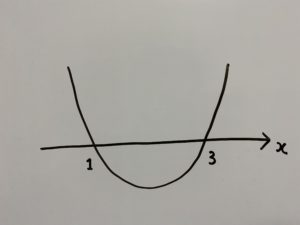
今回は$\leqq$ではなく$\lt$ということに注意しましょう。
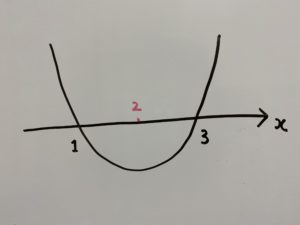
答えは$x=2$
$y=x^2+2kx-k+2$が$y$の値が常に正の時、定数$k$の範囲を求めなさい。
２通りの解法を紹介します。
解①（二次関数の頂点から求める）
まずはこの観点から答えを導きます。
頂点の求め方を忘れてしまった方は、下の記事をご覧ください。
$(与式)=\{(x^2+2kx+k^2)-k^2\}-k+2=(x+k)^2-k^2-k+2$
よってこの式の頂点は$(-k,-k^2-k+2)$
またこの二次関数は下に凸。したがって$y$の値が常に正であるためには
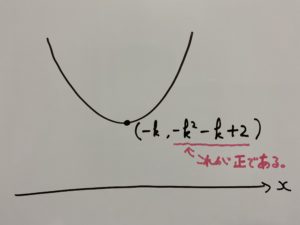
のように頂点の$y$座標が正である必要があります。
つまり$-k^2-k+2 \gt 0$ですね！これを解くと
$k^2+k-2 \lt 0$
$(k+2)(k-1) \lt 0$
$-2 \lt k \lt 1$
解②（判別式から求める）
この方法でも可能です。なぜなら、今回のような下に凸のグラフにおいて、$D \lt 0$の場合
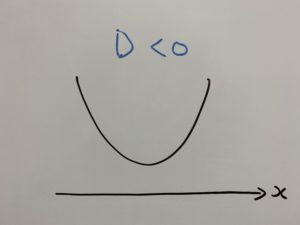
のようになるからです。$x$軸との交点が存在しないわけですから。
したがって
$D=(2k)^2-4 \times 1 \times (-k+2)=4k^2+4k-8 \lt 0$
$k^2+k-2 \lt 0$
$(k+2)(k-1) \lt 0$
$-2 \lt k \lt 1$
最後に
みなさんいかがでしたか？分かりましたか？
このブログは『数学が苦手な方』向けに作成しております。
なので懇切丁寧な記事を心掛けておりますが、みなさんしっかり理解できているかたまに心配になります笑
私ジルにとっての”分かりやすい”とみなさんにとっての”分かりやすい”は違うかもしれないですのでね(・Д・)
これからも分かりやすさにこだわって記事を書き続けようと思いますのでごひいきによろしくお願いします(*´∀｀*)
