みなさんおはこんばんにちは!
花粉でくしゃみが結構出るジルでございます。
今回は二次不等式について解説します。
グラフの画像を使いながら分かりやすい記事にしましたので最後までご覧ください!
二次不等式の解

最後にまとめますね( ^ω^ )
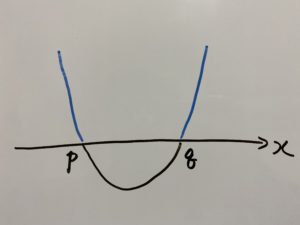
こういうグラフの場合ですね!
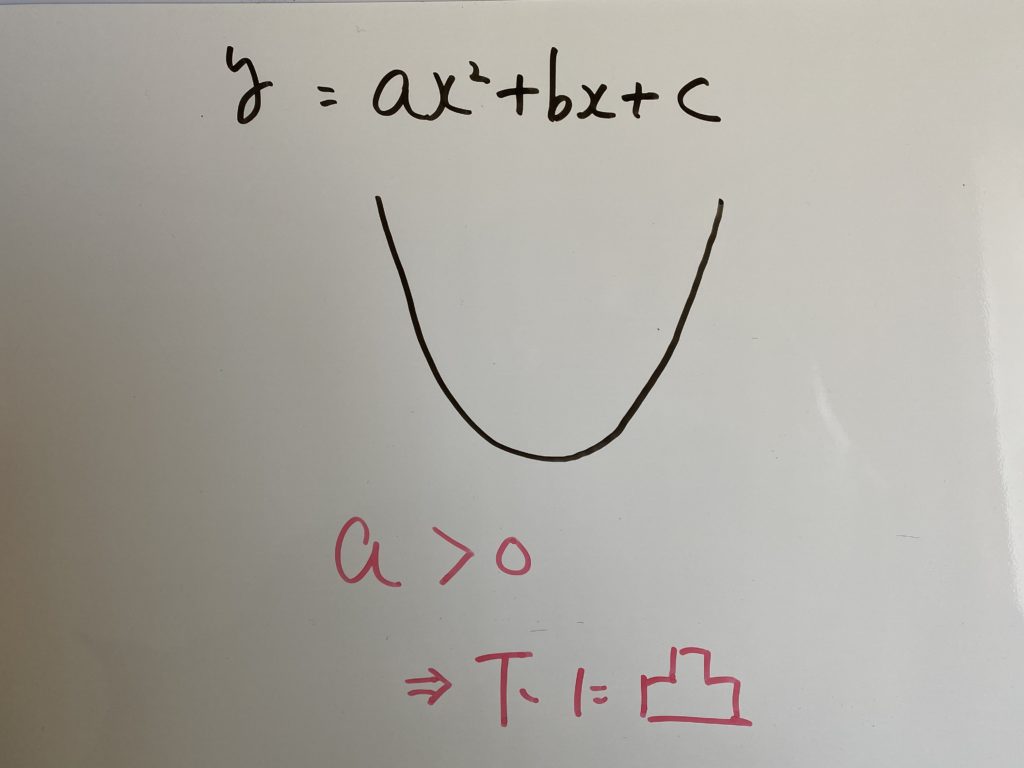
判別式別に考えます。
この場合、次のグラフのように交点が2つあるパターンになります。
今回この2つの交点の
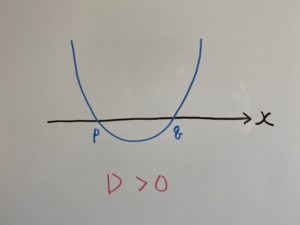
次の3パターンの場合を考えます。
(ⅰ)
(ⅱ)
(ⅲ)
(ⅰ)
これはグラフを見れば明らかで、青色の部分になります。
つまりこれを満たす
(ⅱ)
こちらはグラフの青色の部分になります。
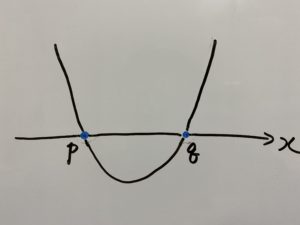
つまりこれを満たす
(ⅲ)
こちらはグラフの青色が付いている部分になります。
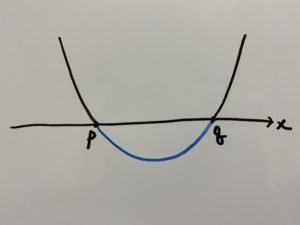
つまりこれを満たす
この場合次のグラフのように交点が1つになります。
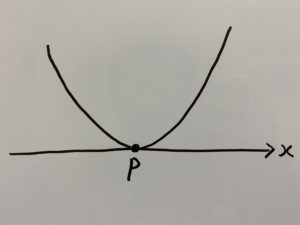
では先ほどと同様に次の3パターンの場合を考えます。
(ⅰ)
(ⅱ)
(ⅲ)
(ⅰ)
青色が付いている部分になります。
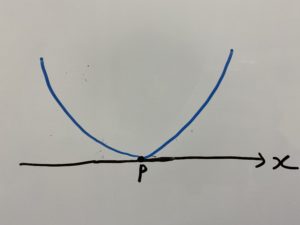
つまりこれを満たす
(ⅱ)
こちらはグラフの青色が付いている部分になります。
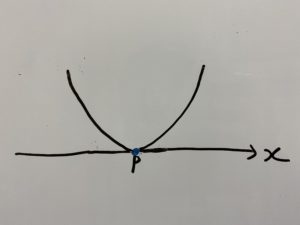
つまりこれを満たす
(ⅲ)
グラフを見てもらうと分かりますが、
この場合は
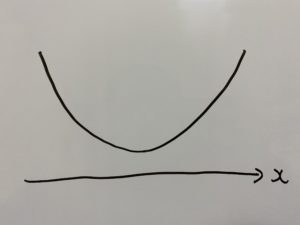
(ⅰ)
(ⅱ)
(ⅲ)
で考えてみましょう!
とはいうものの、グラフ見て分かる通り、全部(ⅰ)なんですね!なので全範囲において(ⅰ)です。
![]()
こういうグラフの場合ですね!
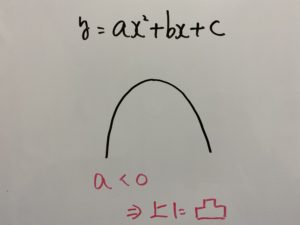
判別式別に考えます。
この場合、次のグラフのように交点が2つあるパターンになります。
今回この2つの交点の
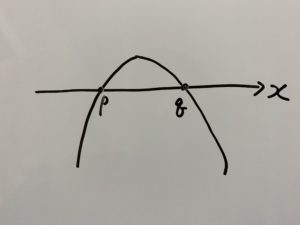
次の3パターンの場合を考えます。
(ⅰ)
(ⅱ)
(ⅲ)
(ⅰ)
これを満たす範囲は青色の付いた部分ですね!
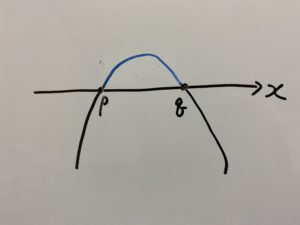
したがって、
(ⅱ)
この場合は青色の付いた部分ですね
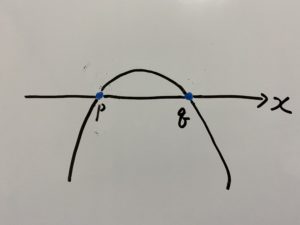
したがって
(ⅲ)
次の部分ですね。
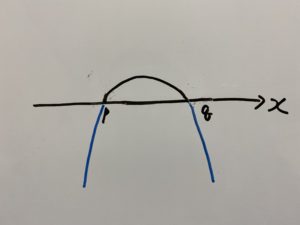
したがって
この場合次のグラフのように交点が1つになります。
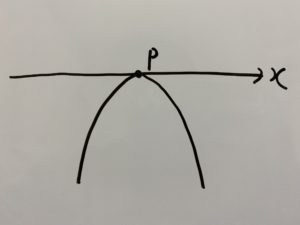
では先ほどと同様に次の3パターンの場合を考えます。
(ⅰ)
(ⅱ)
(ⅲ)
(ⅰ)
これを満たす部分はありません!
(ⅱ)
こちらの、青色が付いた部分になります。
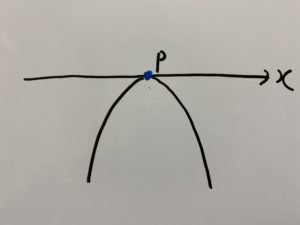
したがって
(ⅲ)
はいこの部分です!
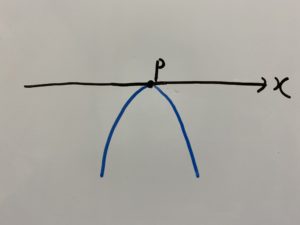
したがって、
この場合は
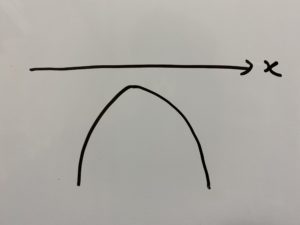
(ⅰ)
(ⅱ)
(ⅲ)
で考えてみましょう!
とはいうものの、グラフ見て分かる通り、全部(ⅲ)なんですね!なので全範囲において(ⅲ)です。
二次不等式の範囲のまとめ
最後に
今回は長々と二次不等式について解説しました。
次回から実際に問題を解いていきたいと思います。