みなさんおはこんばんにちは。
コタツ欲しいけど絶対堕落するから買おうか迷っているジルでございます！
今回は高校数Iの『二次不等式』の問題を解いていきたいと思います！
まずは基本問題からです。
ちなみに基礎がまだ身についていない方はこちらの記事をご覧ください。
では早速いってみよう！
問１ 次の二次不等式を解きなさい。
まずは基礎中の基礎の問題です。これができなきゃ始まりませんので確実に全問正解できるようにしましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
$(1) x^2-4x+3 \gt 0$ $(2) 3x^2-2x-3 \geqq 0$
$(3) 2x^2-5x+1 \leqq 0$ $(4) 2x^2-x+3 \lt 0$
この４問を解いてみます。
【苦手な方向け】
私が考える解き方の手順はこちらです。
では解いてみましょう。
$x^2-4x+3 \gt 0$
先ほど書いた順序で解いてみます。
①$x^2$の項は$1$、つまりプラスです。したがってこのグラフは下に凸ですね！
②左辺の判別式は$D=(-4)^2-4 \times 1 \times 3=16-12=4 \gt 0$
したがって今回の二次不等式は$x$軸と２つの交点を持ちます。
③$x^2-4x+3=0$を解いてみましょう。こちらは簡単に解けますね！
$(x-3)(x-1)=0$となり、$x=3,1$ですね。
④上記の情報からグラフを書くと次のようになります。
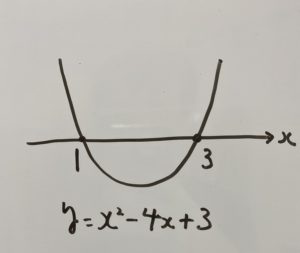
⑤次の部分になりますね！
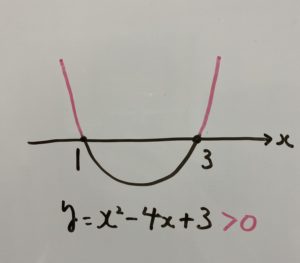
したがって$x \lt 1,3 \lt x$
$３x^2-2x-3 \geqq 0$
①$x^2$の項は$3$、つまりプラス。したがって下に凸ですね。
②判別式は、$D=(-2)^2-4 \times 3 \times (-3)=4+36=40 \gt 0$
したがって$x$軸との交点は2つです。
③$3x^2-2x-3=0$を解いてみましょう。
解の公式を用いましょう！
$x=\frac{2\pm\sqrt{(-2)^2-4 \times 3 \times (-3)}}{2 \times 3}=\frac{2\pm\sqrt{40}}{6}=\frac{2\pm2\sqrt{10}}{6}=\frac{1\pm\sqrt{10}}{3}$
④グラフを書くとこんな感じです。
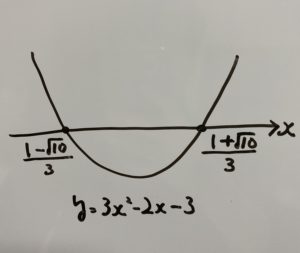
⑤範囲はこちらになります。
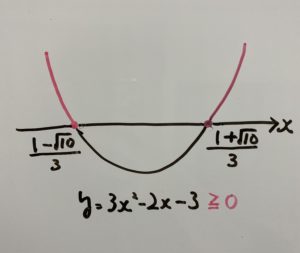
したがって答えは $x \leqq \frac{1-\sqrt{10}}{3},\frac{1+\sqrt{10}}{3} \leqq x$
$-2x^2-5x+1 \gt 0$
①$x^2$の項は$-2$なのでマイナス。したがって上に凸です。
②左辺の判別式を解きましょう。
$D=(-5)^2-4 \times (-2) \times 1=25+8=33 \gt 0$
③$-2x^2-5x+1=0$を解いてみましょう。
$x=\frac{5\pm\sqrt{(-5)^2-4 \times (-2) \times 1}}{2 \times (-2)}=\frac{5\pm\sqrt{33}}{-4}=\frac{-5\pm\sqrt{33}}{4}$
④グラフを書くと次のようになります。
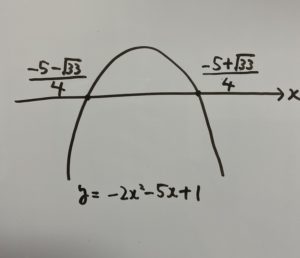
⑤範囲は次のようになります。
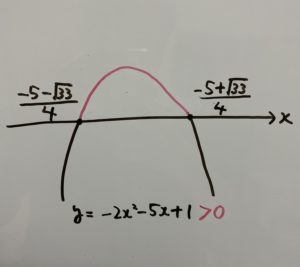
したがって答えは$\frac{-5-\sqrt{33}}{4} \lt x \lt \frac{-5+\sqrt{33}}{4}$
$２x^2-x+3 \lt 0$
①$x^2$の項は$2$なのでプラス。したがって下に凸です。
②左辺の判別式は
$D=(-1)^2-4 \times 2 \times 3=1-24=-23 \lt 0$
③$2x^2-x+3=0$を解いてみます。
…といいたいところですが、今回は解かなくても問題解けますのでスキップします。
④グラフはこんな感じ
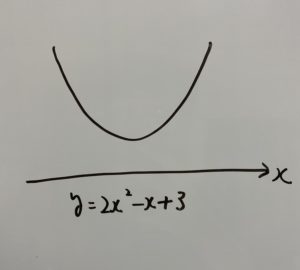
⑤上のグラフを見てもらえば分かりますが、$y=2x^2-x+3 \lt 0$の部分がないんですね。
したがって答えはなしです。
最後に
この手順はできるようにしましょう。
自然とこれができるようにたくさん問題を解きましょう！
次は応用問題を解説しようかと思います。
楽しい数学Lifeを！
