【高校数I】二次方程式の基礎を元数学科が解説【苦手克服】

今回から二次方程式の分野をやっていきます。

とりあえず基礎を一緒に確認しましょう( ^ω^ )

 

そもそも二次方程式とはなんぞや？

数学が苦手な方、ここから見ましょう。

もう分かるよ！って方はすっ飛ばしちゃってください。

$$ax^2+bx+c=0$$

この形の方程式を二次方程式と言います。

二次方程式なので実数解は最高で２つあります。１つの場合（重解）、解がないパターンもあります。

 

 

二次方程式を解く方法

では二次方程式を解く方法を紹介します。

大きく分けて２つあります。

因数分解して解く

まずはこちら。

以前に学んだ因数分解を利用した解き方です。

$ax^2+bx+c=0$において、

$ax^2+bx+c=(px+q)(rx+s)$

と因数分解できるならば、

$(px+q)(rx+s)=0$となりますから、$px+q=0$または$rx+s=0$であればいいですね？

$px+q=0$の時

$px=-q$

$x=-\frac{q}{p}$

$rx+s=0$の時

$rx=-s$

$x=-\frac{s}{r}$

よって解は$x=-\frac{q}{p}$、$x=-\frac{s}{r}$ となります。

 

『因数分解』を利用して解ける二次方程式を１つやってみましょう。

 

 

「$４x^2-18x+8=0$」を『因数分解』を用いて解く。

こちらを解きましょう。

『たすきがけ』を使います。覚えていますか？忘れちゃった方のために記事を貼っておくのでよかったらご覧ください。

 

因数分解のたすきがけを元数学科が詳しく解説する。【苦手克服】

みなさん因数分解の「たすきがけ」は上手く使いこなせていますでしょうか？複雑な問題に対してたすきがけは解くのに大変有効な手段となります。ただし数学が苦手な人には始めは抵抗があるでしょう。たくさんの問題を解いて技術を身につけましょう！

www.zilleblog.com

2020.06.20

 

私ならこう解く

こうですね。ではやってみましょう。

 

①全部の項が２の倍数なのは分かりますか？

よって割ります。

$4x^2-18x+8=0$

　　　 ⇩（2で割る）

$2x^2-9x+4=0$

 

②たすきがけを使いましょう。

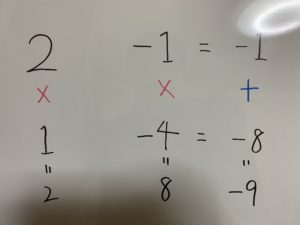
したがって

$2x^2-9x+4=0$

　　　 ⇩（たすきがけ）

$(2x-1)(x-4)=0$　　　　

これで$x=\frac{1}{2},4$であることが分かりました。

 

 

『解の公式』を利用して解く

こちらがよく使われる手法です。

この公式は覚えましょう。

$ax^2+bx+c=0$の解は

$$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$$

であります。

ただしこれ、実は条件がありまして、

 

$$b^2-4ac \geqq 0$$

でなくてはいけません。これは先ほどの解の公式のルートの中です。

ルートの中は正数でなくてはいけませんね？だからです。

 

では『解の公式』を使って先ほど因数分解で用いた問題を解いてみましょう。

「$４x^2-18x+8=0$」を『解の公式』を用いて解く。

解の公式を使います。

今後何度も使うことになるので絶対に覚えましょう！

①全ての項が２の倍数なので２で割ります。

$4x^2-18x+8=0$

　　　⇩（２で割る）

$2x^2-9x+4=0$

 

②解の公式に当てはめてみましょう。

 

$x=\frac{-(-9) \pm \sqrt{ (-9)^2-4\times2\times4 }}{4}$

$=\frac{9 \pm \sqrt{ 81-32 }}{4}$

$=\frac{9 \pm 7}{4}$

したがって$x=\frac{1}{2},4$

 

最後に

今回は二次方程式の入りの部分を書きました。

記事内で何度か言っていますが、

『解の公式』は必ず覚えましょう。

覚えなくても別にいい公式も割と存在しますが、この公式は覚えるべきです。

次回は『判別式』についての記事を書く予定です。