【高校数A】方べきの定理を元数学科が解説する！【苦手克服】

方べきの定理について解説していきます。

しかし高校数学では噛み砕いて簡単にまとめてありますのでご安心ください！

 

このブログではは他の参考書よりも丁寧を心掛けております。

 

方べきの定理①

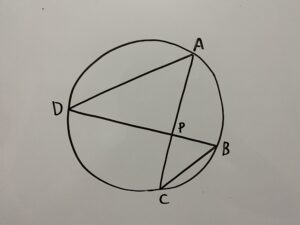
この時

$PA \times PC=PB \times PD$

が成立する。

 

証明

まず円周角の定理より

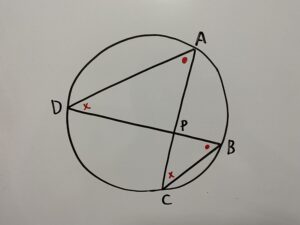
が成立します。

ここでみなさん『三角形の相似』について覚えていますか？？

今回出てきた△PADと△PBCは３つの条件の中で”③２組の角がそれぞれ等しい”を満たしております。

したがって$△PAD \backsim △PBC$であります。

相似であると言うことは辺の比が等しいと言うことですよね？

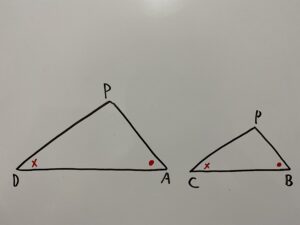
つまり

$PA:PB=PD:PC$

$PA \times PC=PB \times PD$

 

方べきの定理②

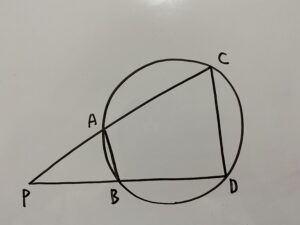
この時

$PA \times PC=PB \times PD$

が成立する。

 

証明

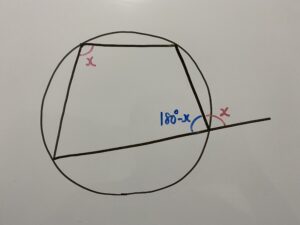
この証明を解くには以前記事でご紹介した『円に内接する四角形に関する定理』を使う必要があります。

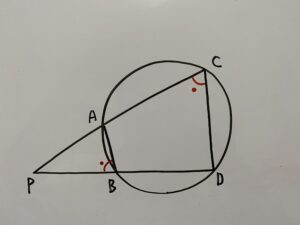
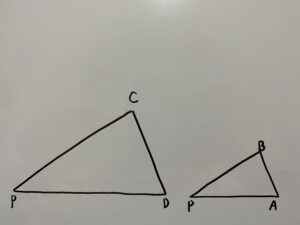
方べきの定理③

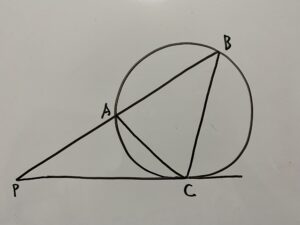
証明

 

 

$△PAC \backsim △PCB$を証明すればOKです。

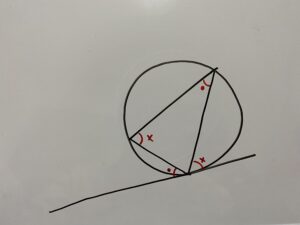
ここで一つ。”円に内接する三角形に関する定理”を学びましょう！

因みにこれを巷では『接弦定理』といいます。

では本題の証明に戻ります。

△PACと△PCBについて

$\angle APC=\angle CPB$は明らかですね？同じ角のことを言っていますから。

次に”円に内接する三角形に関する定理”より

$\angle PCA=\angle PBC$

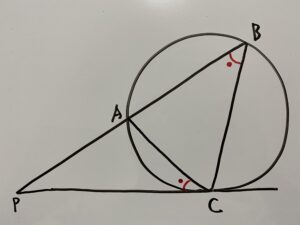
が成立します。よって”２組の角がそれぞれ等しい”ので

$△PAC \backsim △PCB$

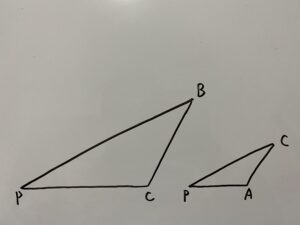
したがって

$PA:PC=PC:PB$

$PA \times PB=PC^2$

 

練習問題

では練習問題を解いてみましょう。

第１問

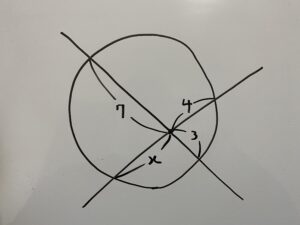
この時xの値を求めなさい。

 

方べきの定理①を使うと解けます。

この定理を覚えていればもう楽勝ですね。

 

$4 \times x=7 \times 3$

$4x=21$

$x=\frac{21}{4}$

 

答え：$\frac{21}{4}$

 

第２問

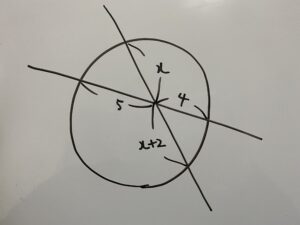
この時xの値を求めなさい。

 

先程の少し応用編です。

$x \times (x+2)=5 \times 8$

$x(x+2)=40$

$x^2+2x-40=0$

$x=\frac{-2 \pm \sqrt{2^2 – 4 \times 1 \times (-40)}}{2}=\frac{-2 \pm \sqrt{164}}{2}=-1 \pm \sqrt{41}$

ここでxが$-1 + \sqrt{41}$か$-1 – \sqrt{41}$どちらかと言う話ですが、今回のxが正の数であることはわかりますか？

$\sqrt{36} \lt \sqrt{41} \lt \sqrt{49}$より

$6 \lt \sqrt{41} \lt 7$

よって$-1 – \sqrt{41} \lt 0$、$-1 + \sqrt{41} \gt 0$

よって$x=-1 + \sqrt{41}$

答え：$x=-1 + \sqrt{41}$

 

第３問

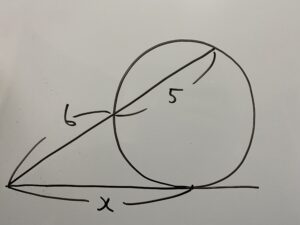
この時xの値を求めなさい。

 

こちらは方べきの定理③を使うことで簡単に解けます。

ではこの定理に数字を当てはめてみましょう！

$6 \times (6+5)=x^2$

$66=x^2$

$x= \pm \sqrt{66}$

xは正の数なのは明らかなので$x=\sqrt{66}$

答え：$\sqrt{66}$

 

第４問

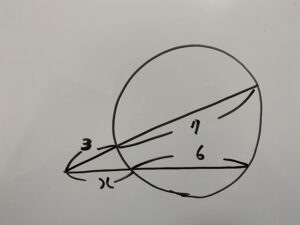
この時xの値を求めなさい。

 

方べきの定理②を使って解く問題ですね。

ではとっとと当てはめてみましょう。

$3 \times (3+7)=x \times (x+6)$

$30=x^2+6x$

$x^2+6x-30=0$

解の公式より

$x=\frac{-6 \pm \sqrt{36-4 \times 1 \times 30}}{2}=\frac{-6 \pm \sqrt{156}}{2}=\frac{-6 \pm 2\sqrt{39}}{2}=-3 \pm \sqrt{39}$

$\sqrt{39}$について、$\sqrt{36} \lt \sqrt{39} \lt \sqrt{49}$

よって$6 \lt \sqrt{39} \lt 7$

つまり$-3 – \sqrt{39} \lt 0$、$-3 + \sqrt{39} \gt 0$

xは正の数であることは明らかなので

$x=-3 + \sqrt{39}$

答え：$-3 + \sqrt{39}$

 

まとめ