
みなさんおはこんばんにちは。
最近体調不良から回復したジルでございます!
今回は確率論の中の『順列』について解説します。
同じものを含む順列
重複順列
円順列
じゅず順列
順列の定義
異なるn個のものからr個を取り出して1列に並べることを順列と言います。
順列の個数を
例えば「A,B,C,D,Eから3個選んで並べる」順列の個数は
次に
これをもう少し簡略化して表すと
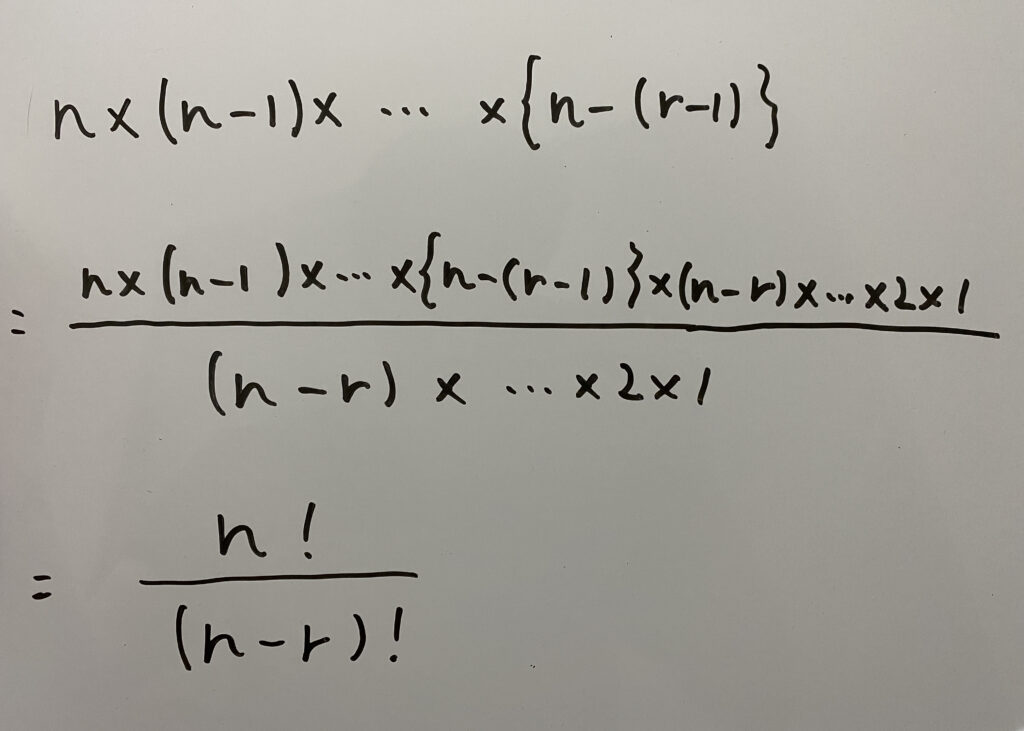

これ覚えときましょう(^∇^)
では先ほど例に出した「A,B,C,D,Eから3個選んで並べる」順列の個数
ちなみに…

ではいくつか練習問題を解いてみましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
練習問題①
次を計算してください。
(1)
(2)

順列の問題で一番基本的な問題です。
一瞬で解けるようになるまで繰り返し練習しましょう。
(1)の解答
(2)の解答
練習問題②
0,1,2,3,4のうち、4つ選んで4桁の数字を作る。その場合の数はいくつあるか。
もう一歩進んでみましょう。

分かった!5つの数字から4つ選んで並べるから
一見それで解けそうですがこれだと間違いです。
なぜなら
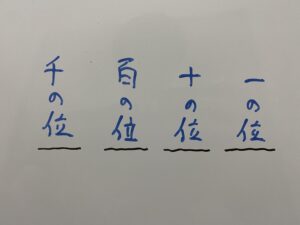
の中の「千の位」が0だと4桁にならないからです。
よってそれぞれに入るのは

この場合どう解くか。一、十、百の位は0,1,2,3,4から、千の位だけ 1,2,3,4からなので千の位から決めてそのあと他の位を計算する方法がいいでしょう。
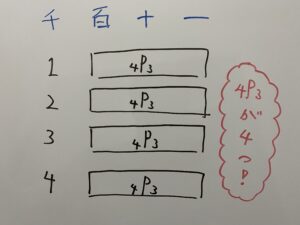
したがって
答えは96
同じものを含む順列
ここからはすこーしだけ特殊な順列のパターンを解説していきます。
特殊といってもそんなに難しくなく、テストにもよく出ますので理解しましょう。
まずは「同じものを含む順列」です。
先程は同じものを含まないパターンをやってきましたね?
この場合は公式がありまして
その並べ方の総数は

このあと別記事で解説予定の『組み合わせ』を学ぶとこの公式をより深く理解できます!
『組み合わせ』についての記事を書く際には触れていく予定です( ^ω^ )
いくつか練習問題を解いてみましょう!
練習問題③
1,1,2,2,2,3,3を全て使って7桁の数字を作る時、その並べ方は何通りか答えなさい。
7個のうち、同じものが2個、3個、2個あるので
答えは210通り。
重複順列
先ほどの『同じものを含む順列』と日本語としては少し近いですが違います。
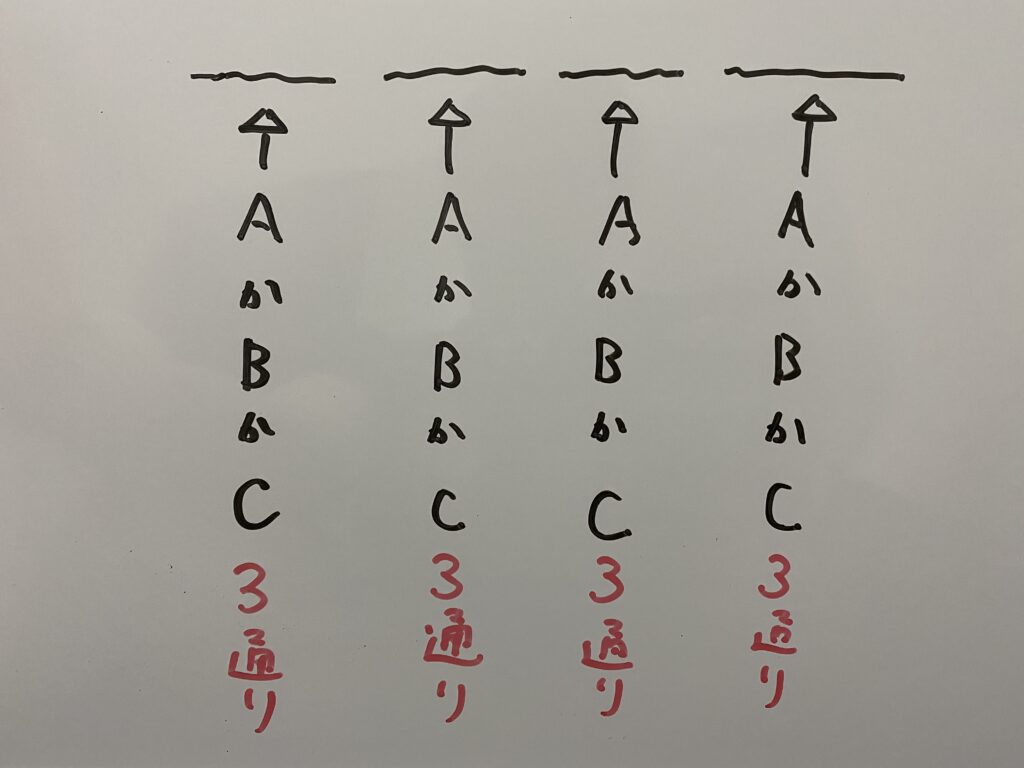
練習問題④
4人が1回じゃんけんをします。その時手の出し方は何通りあるか答えなさい。
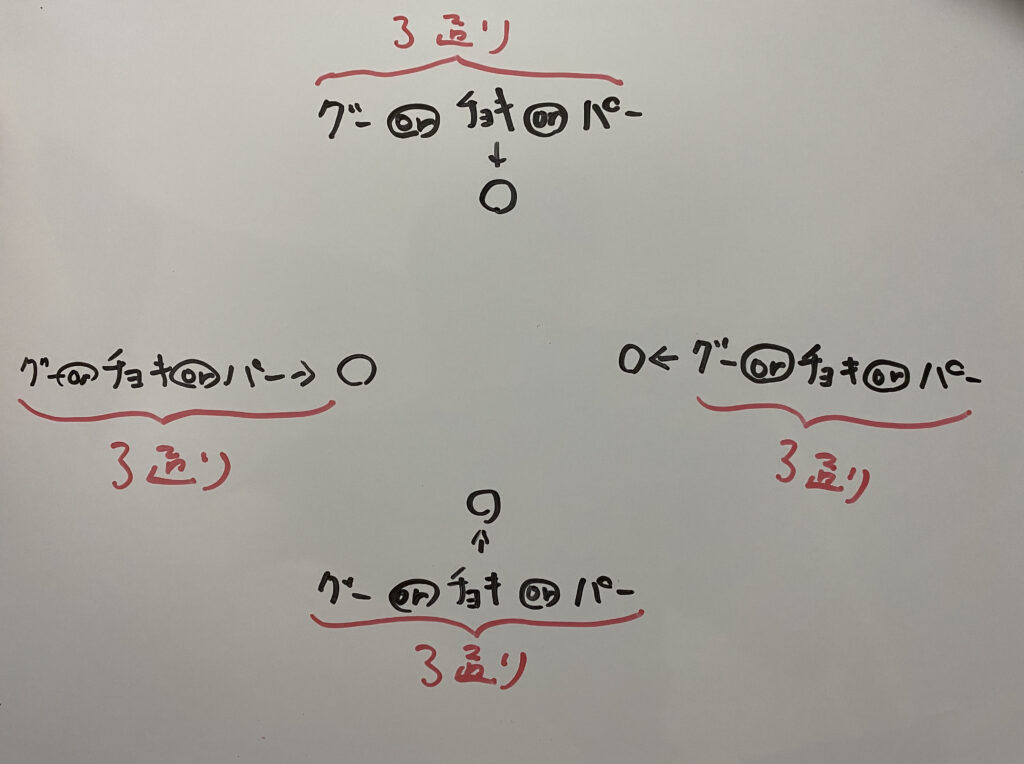
こういうことですね。つまり
答えは64通り。
練習問題⑤
コインを6回投げます。その時、表と裏の出方は何通りか答えなさい。
図のように考えます。

したがって
答えは64通り。
円順列
こちらは名前の通り、円の形に並べた場合になります。
例えば
A,B,C,D,Eを円形に並べる時その場合の数は何通りか。
このような問題です。
そもそも『円順列』がなぜ普通の順列と考え方を変えなければならないかといいますと
例えば円形にせずにそのまま1列に並べる場合
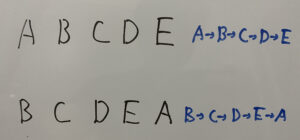
この2つは違う場合になりますね?
しかし円順列の場合
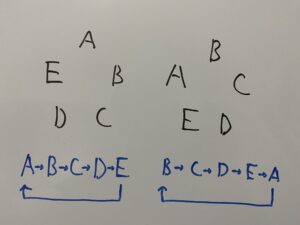
この2つは一緒の場合になるのです。

くるっと回して貰えばわかります。
まず円にせず一列にA,B,C,D,Eを並べる場合その場合の数は5!通りですね?
その列の先頭と最後尾を結んでみましょう。
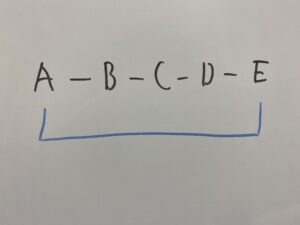
ここで気づいて欲しいのは
A,B,C,D,EとB,C,D,E,AとC,D,E,A,BとD,E,A,B,CとE,A,B,C,Dは全て円順列にすると一緒になるということです!
他の場合も
B,A,C,D,EとA,C,D,E,BとC,D,E,B,AとD,E,B,A,CとE,B,A,C,D
C,A,B,D,EとA,B,D,E,CとB,D,E,C,AとD,E,C,A,BとE,C,A,B,D
などなど…
全て5通り被る場合が存在する訳です。
なので一緒の場合を省くには5で割ればいい訳ですね!
したがって円順列の求め方は
では公式をまとめます。
練習問題⑥
次のような円を5分した図形にそれぞれ異なる色を塗る。塗り方の場合の数の総数は何通りか。
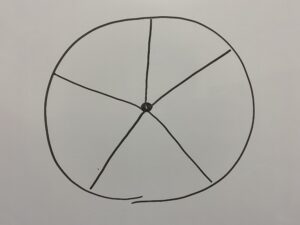
こちらは6種類の円順列なので
答えは24通り。
練習問題⑦
コーチ2人と子供6人で円形の机の周りに座る。この時
(1)コーチ2人が隣り合って座る場合の数は何通りあるか。
(2)コーチ2人が向かい合って座る場合の数は何通りあるか。
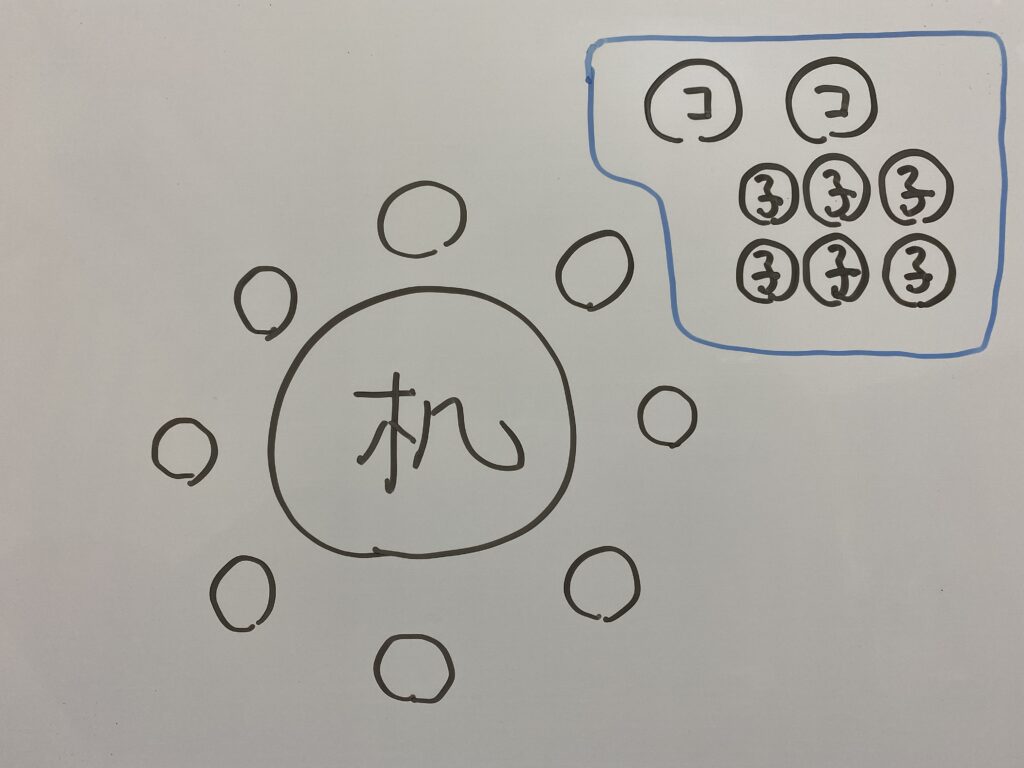
(1)この場合はコーチ2人を1つにまとめて考えるといいです。
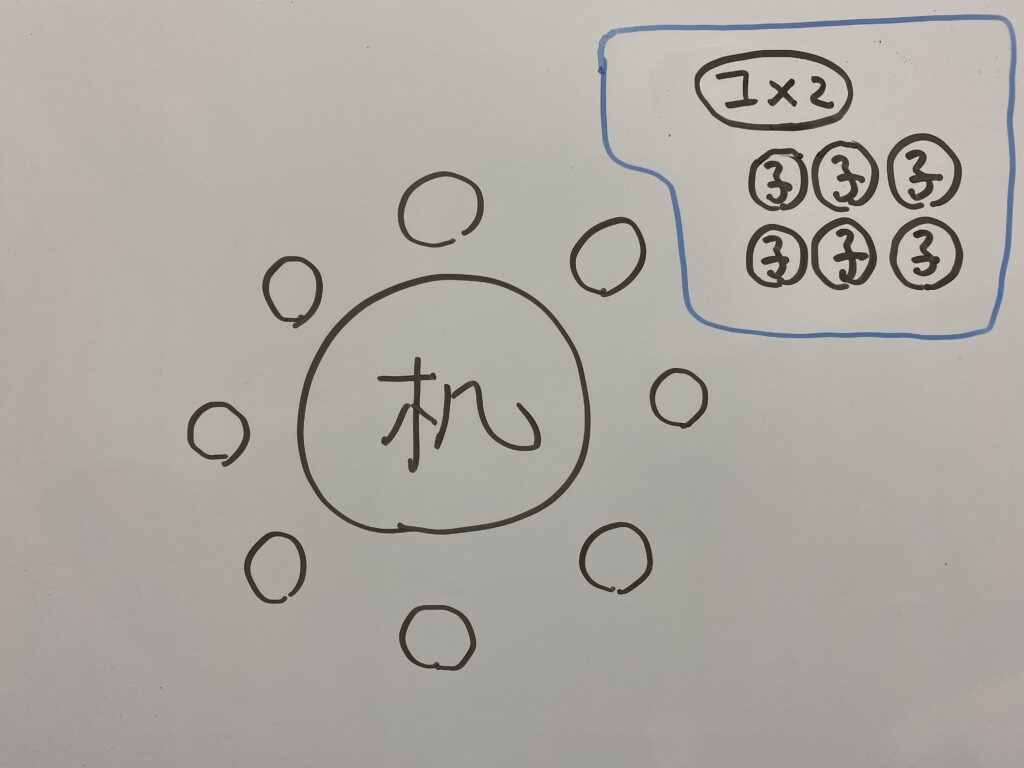
こう書くと7つのものに関する円順列になります。
7つのものに関する円順列の場合の数は
あとはコーチについて
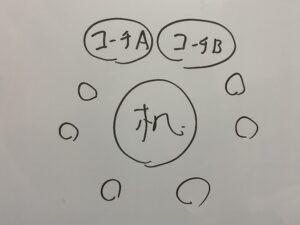
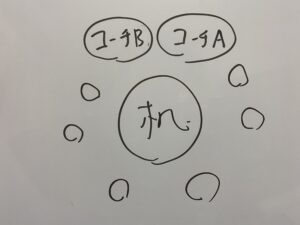
この2パターンがあるので
答えは1440通り。
(2)まずは子供6人を席に座らせましょう。
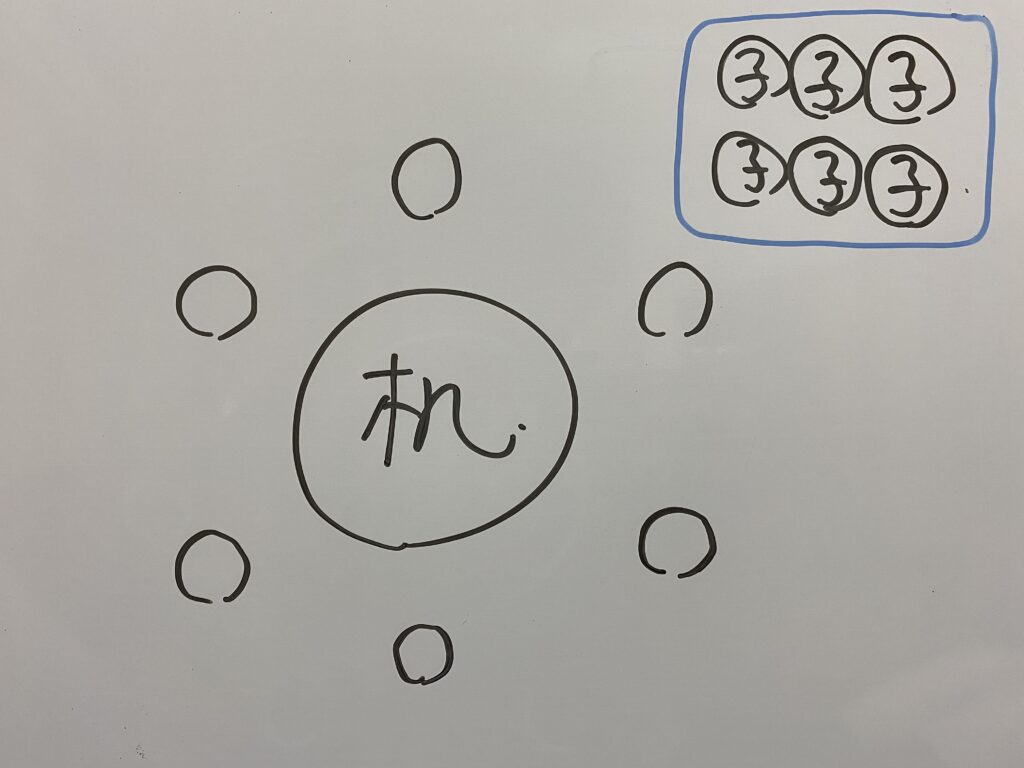
6つのものに関する円順列になるので
次にコーチ2人を子供達の間に座らせます。
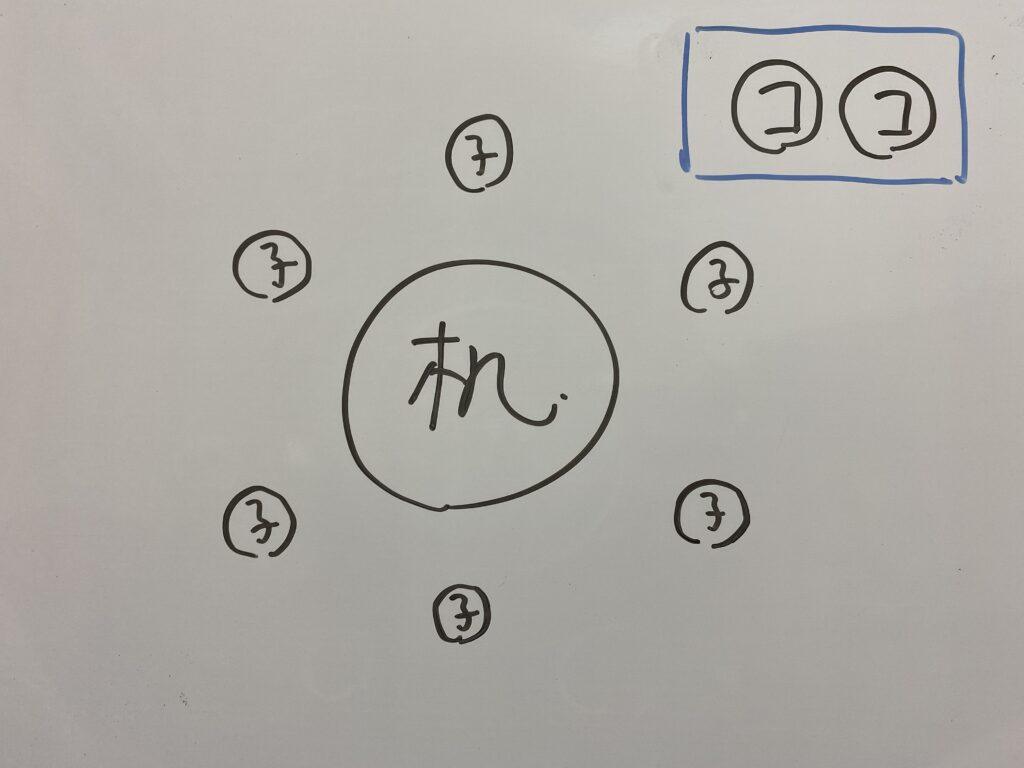
その座り方は6通りですね?したがって
答えは720通り。
じゅず順列
こちらは円順列の中でも、裏返して重なるものを同じとみなした場合の順列のことです。
裏返した場合を同じにするため、円順列の公式を2で割ればいい訳です!
練習問題⑧
それぞれ色の異なる珠7個を使ってじゅずを作る時、何通りのじゅずができるか答えなさい。
じゅず順列の公式
答えは360通り。
まとめ
n個のうち、同じものがa個、b個、c個、…あるものとする。
その並べ方の総数は
異なるn個ものから同じものを繰り返しとってもいいものとしてr個とる場合の総数は
異なるn個のものを円形に並べた時その場合の数は
異なるn個のものに関して、そのじゅず順列は

楽しい数学Lifeを!



