みなさんおはこんばんにちは。
この頃明太子にハマっているジルでございます！
今まで『順列』『組み合わせ』の基礎を解説してきました。
まだみていない方は見てみて！
今回はこの辺りの分野で頻出する問題パターンを解説しようかと思います(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
文字の並べ方の問題
まずは文字が用意されていて、その並べ方を求める問題です。
こちらは比較的簡単な問題です。しっかり解けるようにしておきましょ！
練習問題①
次の文字を一列に並べる並べ方は何通りあるか答えなさい。
（１）QUESTION
（２）ZILLEBLOG
こちらの問題まずなにすれば良いけ？
まずは、その文字列に同じ文字が含まれているかどうかチェックします。
「QUESTION」は重なっている文字はありませんが、「ZILLEBLOG」は「L」が３つ重なっていますね？それぞれのパターンで答えの導き方がすこーしだけ違います。
同じ文字が含まれている⇨$\frac{n!}{a! \times b! \times c! \times …}$
同じ文字が含まれていない場合は順列の基本的な公式$n!$を使えば解けます。
同じ文字が含まれている場合は『同じものを含む順列』の公式を使えば解けます。
n個のうち、同じものがa個、b個、c個、…あるものとする。
その並べ方の総数は
$\frac{n!}{a! \times b! \times c! \times …}$（ただしa+b+c+…=n）
解答
「QUESTION」
８文字の、重なっていない並び替えなので
$8!=8 \times 7 \times 6 \times … \times 2 \times 1=40320$
「ZILLEBLOG」
９文字の、重なっている並び替えなので
$\frac{9!}{3!}=60480$
色分けの問題
図が用意されており、決められた条件で色分けをする問題です。
けっこう色んなパターンの問題があるよねー:(；ﾞﾟ’ωﾟ’):
どうやって解けばいいんさね？
与えられた条件に合うパターンをひとつひとつ書き出してそれぞれの場合の数を計算するしかないです。
こういう解き方をする問題は経験値がものをいいますので、たくさん問題を解きましょうね！
練習問題②
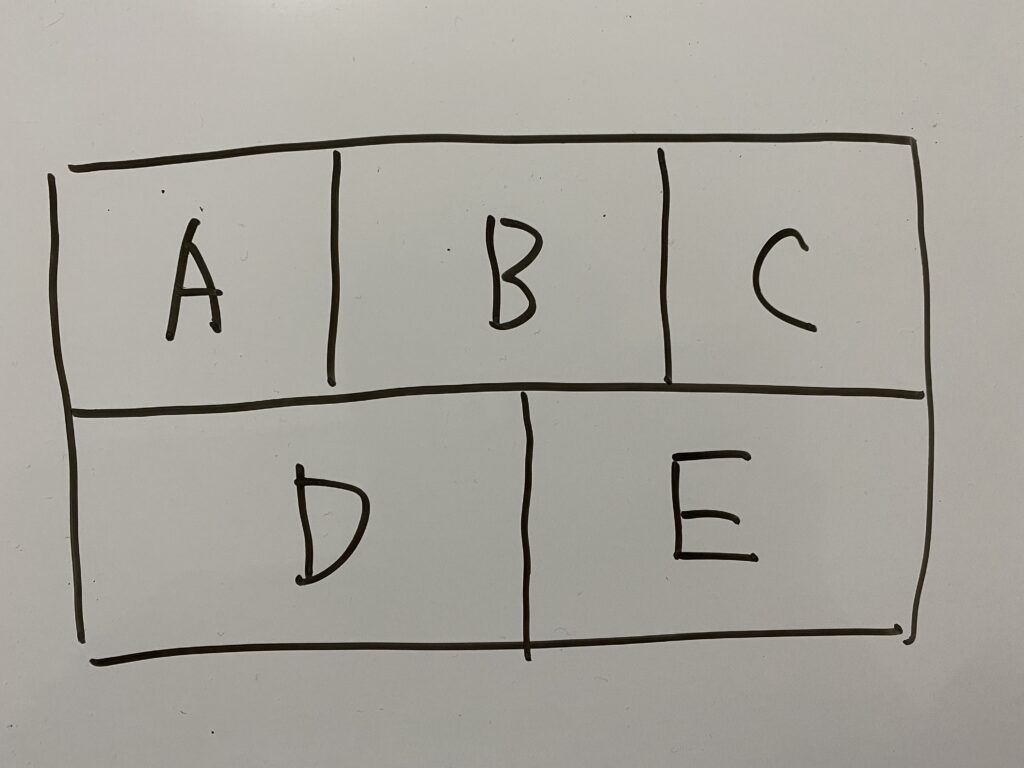
上の図のA,B,C,D,Eに（１）〜（３）の条件で色を塗り分けた時その場合の数は何通りか求めなさい。
ただし、隣り合う部分には同じ色は使ってはいけないものとする。
（１）５色 （２）４色 （３）３色
では早速解いてみましょう。
解答
（１）これはそのまま順列の公式に当てはめればいいです。
${}_5 \mathrm{ P }_5=5!=5 \times 4 \times 3 \times 2 \times 1=120$
答えは１２０通り。
（２）こちらは（１）のように簡単にはいきません。
まずは問題の条件である「４色で、かつ隣同士色が重ならない」パターンを考えてみましょう。
すると次のパターンを考えることができますね？
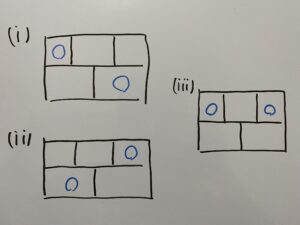
他の色分けのパターンは「４色」または「隣同士色が重ならない」いずれかの条件を満たしていないはずです。
（ⅰ）（ⅱ）（ⅲ）それぞれの色分けの場合の数の求め方について
実は全て同じ求め方でいけます。
最初に○の部分の色を決めます。→４通り
次に残りの部分の色を決めます。→3!通り
これが（ⅰ）（ⅱ）（ⅲ）３パターンあるので
$(4 \times 3!) \times 3=72$
答えは72通り。
（３）こちらも（２）と似た解き方でいけます！
まずは「３色で、かつ隣同士色が重ならない」色分けのパターンを考えてみます。すると
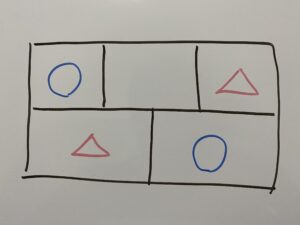
このパターンだけであることが分かります。
では色分けの場合の数の求め方ですが、
最初に○の部分の色を決めます。→３通り
次に△の部分の色を決めます。→２通り
最後に残り一箇所を塗ります。→１通り
別に△の色を決めてから○の色を決めても構いませんので( ^ω^ )
したがって
$3 \times 2 \times 1=6$
答えは6通り。
練習問題③
上の図にそれぞれ違う色で色分けする時その場合の数を求めなさい。
え？全て違う色で塗るとか、さっきの問題の方がむずくね？
ただ5!で解けるやん？？
実は違うんです。
今回注目するところは「円順列になっている」点です！
n個のものを円形に並べた時、その場合の数は
$(n-1)!$
解答
練習問題④
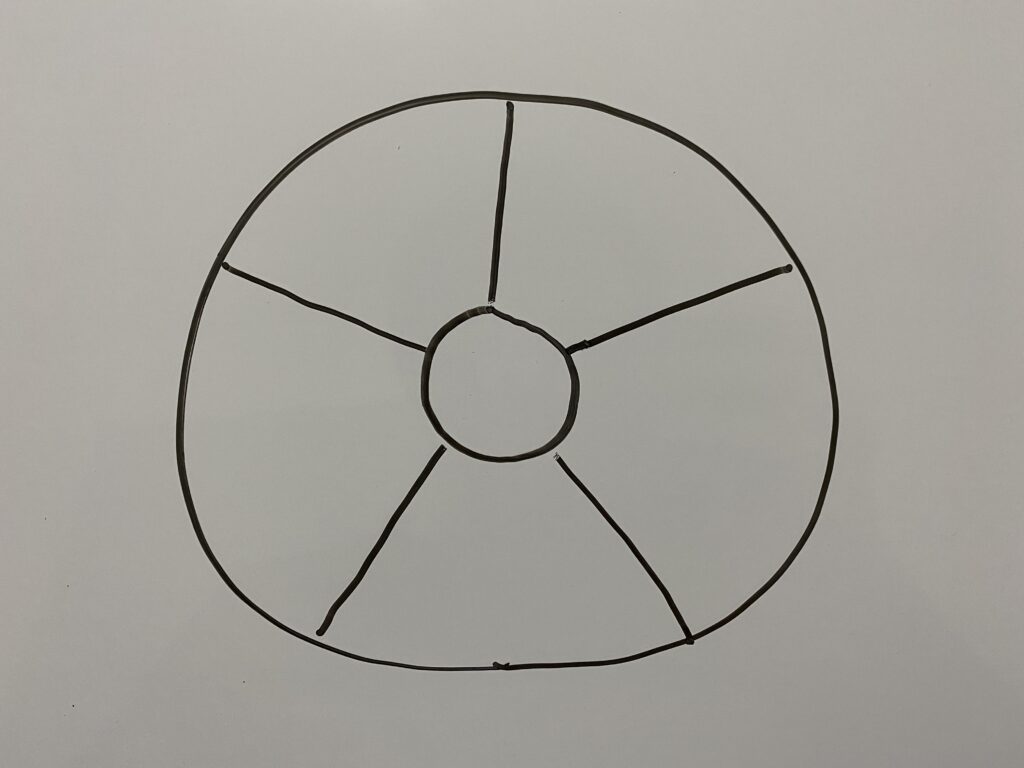
上の図で各部分をそれぞれ違う色で色分けする時その場合の数を求めなさい。
解答
こういうパターンではまず中央の色を決めます。→６通り
あとは周りの色を決めます。→$(5-1)!$通り
したがって
$6 \times (5-1)!=6 \times 4!=144$
答えは144通り。
道順の問題
マス目のような図が用意されており、最短距離でゴールに辿り着く場合の数を求める問題です。
また様々な条件があったりもします。
これけっこう苦手な方多いのではないでしょうか？
練習問題⑤
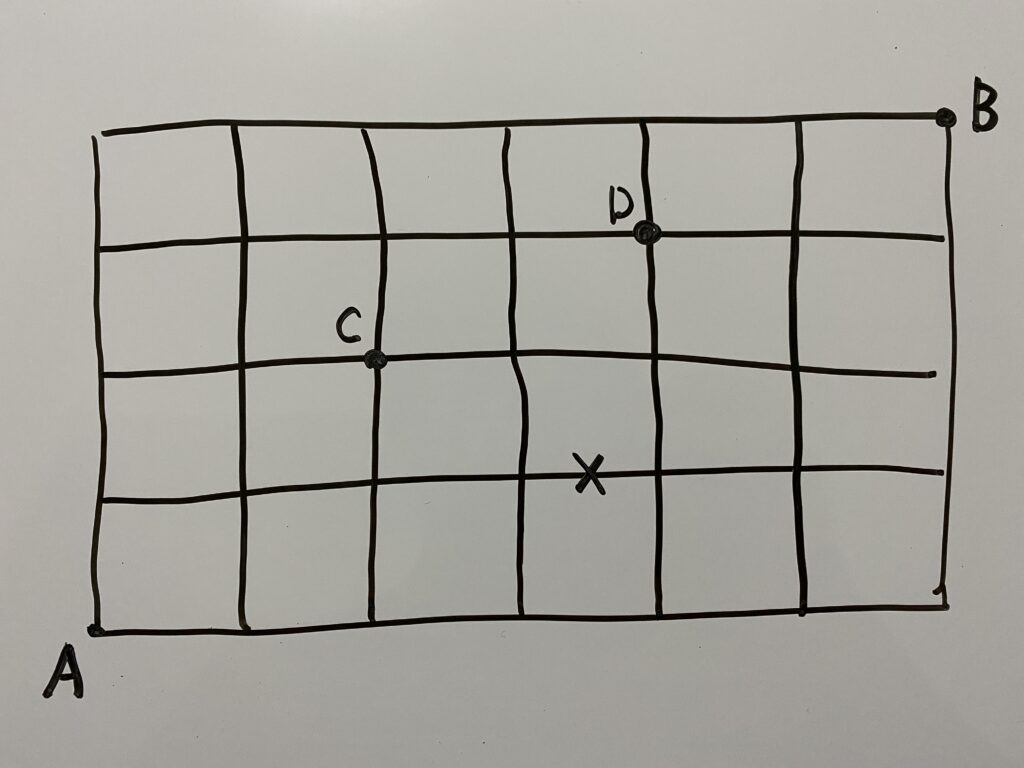
上のような道があり、AからBで最短で向かう。次の問いに答えなさい。
（１）場合の数を求めなさい。
（２）Cを通って行く場合の数を求めなさい。
（３）Dを通って行く場合の数を求めなさい。
（４）C,Dともに通って行く場合の数を求めなさい。
（５）CまたはDを通って行く場合の数を求めなさい。
（６）”×”を通らずに行く場合の数を求めなさい。
６問もありますが、まず共通するポイントは「最短で」行くことです。
今回の問いで最短で向かうためには全ての道で「↑」または「→」の方向に進む必要がありますね？
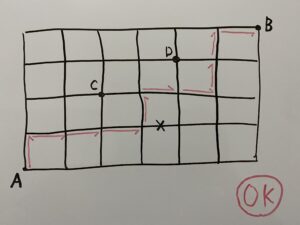
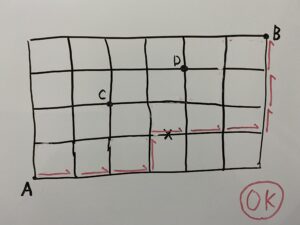
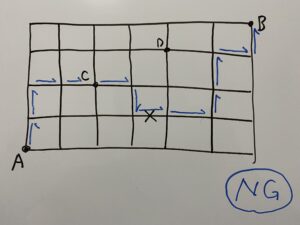
これは道の問題を解く上でとても大事になりますので必ず覚えておいてください！
解答
（１）まず「最短で」とのことなので図より”↑”に４回、”→”に６回進めば最短でBに行けます。つまり、４つの”↑”と６つの”→”における順列の場合の数を求めれば良いので
$\frac{10!}{4! \times 6!}=210$
この計算は『同じものを含む順列』の公式に当てはめたものです。
答えは210通り。
（２）最短でAからBへCを経由して行くため、A→C→Bの順番で通ります。
A→Cの最短ルート、C→Bの最短ルートをそれぞれ考えて積の法則で計算しましょう。
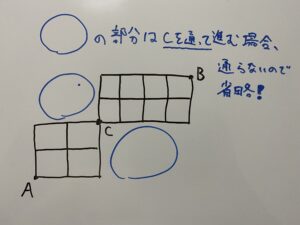
「最短で」という条件が付いているからこそできる考え方ですね( ^ω^ )
・A→Cのルート
“↑”２回、”→”２回、計4回進めば良いので
$\frac{4!}{2! \times 2!}=6$
・C→Bのルート
“↑”２回、”→”４回、計６回進めば良いので
$\frac{6!}{2! \times 4!}=15$
積の法則より
$6 \times 15=90$
答えは90通り。
（３）これは（２）と同じ解き方でいけます。
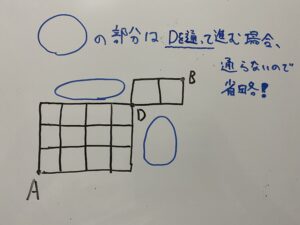
・A→Dのルート
“↑”３回、”→”４回、計７回進めば良いので
$\frac{7!}{3! \times 4!}=35$
・D→Bのルート
“↑”１回、”→”２回、計３回進めば良いので
$\frac{3!}{1! \times 2!}=3$
したがって
$35 \times 3=105$
答えは105通り。
（４）こちらも（２）、（３）の解き方と同じです。
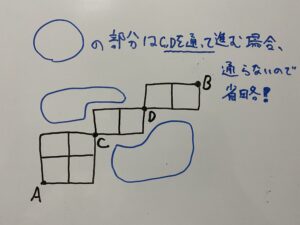
・A→Cのルート
“↑”２回、”→”２回、計４回進めば良いので
$\frac{4!}{2! \times 2!}=6$
・C→Dのルート
“↑”１回、”→”２回、計３回進めば良いので
$\frac{3!}{1! \times 2!}=3$
・D→Bのルート
“↑”１回、”→”２回、計３回進めば良いので
$\frac{3!}{1! \times 2!}=3$
したがって
$6 \times 3 \times 3=54$
答えは54通り。
（５）こちらそのまま解くと結構手間かかります。
少しばかり工夫してみましょうか。
ベン図を描いてみましょう。
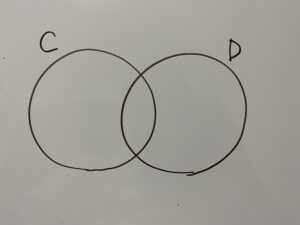
今回求めたいのは$n(C \cup D)$の部分なので
$n(C \cup D)=n(C)+n(D)-n(C \cap D)$
で求められます。
$n(C)$は（２）で求めました。９０通り
$n(D)$は（３）で求めました。１０５通り
$n(C \cap D)は（４）で求めました。５４通り
したがって
$90+105-54=141$
答えは141通り。
（６）こちらは
（最短で行く全てのパターン）-（”×”を通って最短で行くパターン）
を計算すればいいです。
こちら結構出題されるやつです！
（最短で行く全てのパターン）は（１）で求めたので（”×”を通って最短で行くパターン）を求めましょう。
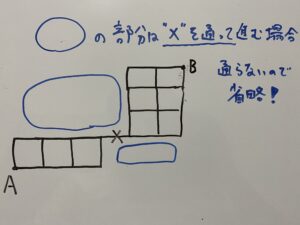
・（ⅰ）のルート
“↑”１回、”→”３回、計４回進めば良いので
$\frac{4!}{1! \times 3!}=4$
・（ⅱ）のルート
“↑”3回、”→”２回、計４回進めば良いので
$\frac{5!}{3! \times 2!}=10$
したがって”×”を通るルートは$4 \times 10=40$
あとは（最短で行く全てのパターン）-（”×”を通って最短で行くパターン）をすれば良いので
$210-40=170$
答えは170通り。
最後に
今回は頻出する問題を取り上げましたが、まだまだたくさんの問題があります。
たくさんの問題を解きましょう。
このブログで口酸っぱくして言ってますが、問題を解いて解いて解きまくるほど上達します。
楽しい数学Lifeを！
