【高校数A】『場合の数』の基礎を元数学科が解説する！【苦手克服】

今回は数Aの「場合の数」についての基礎を解説します。

あたりをやってみます。

 

樹形図

まずは『樹形図』について説明します！

場合の数とは

ある条件下において起こりうる場合の総数

であります。

場合の数を書き出す上で大事な３つがありまして

ここでいくつか場合の数を求めてみましょう！

ex1)表と裏がある２枚のコインを投げた場合の数

まずは全て書き出してみます。

ここで気をつけることは

この２つは同じなんですよ。つまり重複しているわけです。

したがって正しくは

 

 

ex2)Pさん,Qさん,Rさんを一列に並べる場合の数

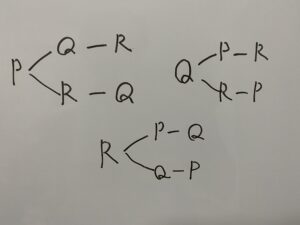
この場合どれも重複していません。

 

 

 

和の法則、積の法則

こちらも重要な要素です。

まずは和の法則から

【証明】

まず赤線の「AとBが同時に起こらない」条件に注目します。同時に起こらないということは

$$A \cap B=\varnothing$$

つまり$n(A \cap B)=0$

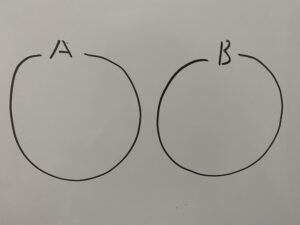
この時AまたはBが起こる場合の数、即ち$n(A \cup B)$は

$$n(A \cup B)=n(A)+n(B)-n(A \cap B)=p+q-0=p+q$$

 

次は積の法則です。

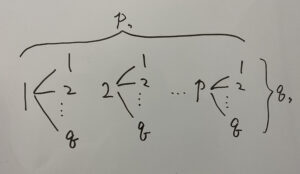
練習問題

いくつか練習問題を解いてみましょう！

問１：展開式の項の数

$(x+y+z)(a+b)$を展開した時の項の数を求めなさい。

２通りの解き方があります。

解１）樹形図を書く

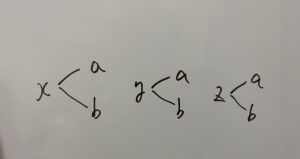
よって６通り。

 

解２）積の法則を使う

この問題（展開式の項の数を求める問題）は積の法則が使えます。

したがって$3 \times 2=6$通り。

 

問２：サイコロの問題

これもよく出てくる問題ですよね。

サイコロAとサイコロBがあります。次の場合の和を求めなさい。

（１）各目の和が８の約数

（２）各目の和が３の倍数

（３）各目の積が９の倍数

「（１）各目の和が８の約数」の解

８の約数を書き出してみましょう。１、２、４、８ですね？

各場合の樹形図を書いてみましょう。

・各目の和が１の場合

みなさんお分かりですかね？こんなのはあり得ません。

・各目の和が２の場合

・各目の和が４の場合

・各目の和が８の場合

それぞれの場合を足して

$1+3+5=9$

したがって答えは9通り。

 

「（２）各目の和が３の倍数」の解

サイコロの目の和の最大値は６＋６＝１２ですね。

１２以下の３の倍数は３、６、９、１２です。

それぞれの場合の樹形図を書いてみましょう。

・各目の和が３の場合

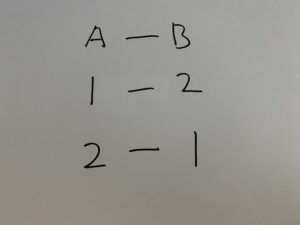
・各目の和が６の場合

・各目の和が９の場合

・各目の和が１２の場合

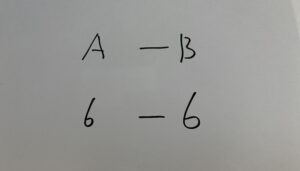
それぞれの場合の和をたして

$2+5+4+1=12$

したがって答えは12通り。

 

「（３）各目の積が９の倍数」の解

各目の積の最大値は6×6=36。

36以下の９の倍数は９、１８、２７、３６。

それぞれの場合の樹形図を書き出してみましょう。

・各目の積が９の場合

・各目の積が１８の場合

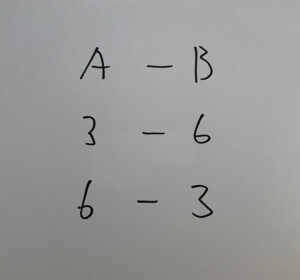
・各目の積が２７の場合

これは存在しません。

・各目の積が３６の場合

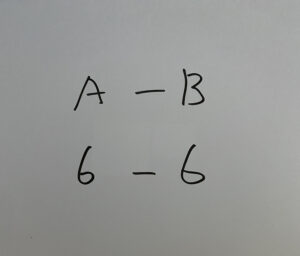
それぞれの場合を足して

$1+2+1=4$

したがって答えは4通り。

 

まとめ