
みなさんこんにちは、ジルでございます!
今回は高校数学で初めの方に学ぶ『因数分解』の解説をしていきます。
こちらは数Iの内容になりますので、文系に進む学生さんも避けて通れないのではないでしょうか?それでいて数学に苦手意識を持っていると結構いやになる単元だと思います笑。
本記事では
・問題の解き方

それではいってみよう!
キホンの確認
因数分解とは!?ってところから
まずは「展開」についておさらいしましょう。
公式は
特定のケースで使える公式
これは共通項がある時にできることです。具体的には
4x²+6x+2=2(2x²+3x+1)
のようなことができます。この考え方はすごく大事です。
問題を解く上で私ジルが考えていること
具体的に問題を解く前に、考えるべき手順を語ります。
これが正しい解き方かわからないので、あくまで「私ならこう解く」手順です。
手順
①問題をじっくり眺める。
②共通項があれば、ab+ac=a(b+c)のようにしてまとめる。
③a²+2ab+b²=(a+b)²
a²−b²=(a+b)(a−b)
の公式が使えるかチェックする。使えれば使って、使えなければ④へ。
④acx²+(ad+bc)+bd=(ax+b)(cx+d) a,b,c,dは定数
を使って解く。
こんなところですかね。
②あるいは③の公式が使える問題なら楽です。
「たすきがけ」について
これは④を用いて解く際に必要な考え方です。
というのも、
x²+6x+8=(x+4)(x+2) とか x²−11x+18=(x−9)(x−2)
レベルの問題なら、数をこなせば頭の中でパッと解けるようになります。
しかし、
6x²+7x−5
のレベルになってくると、パッとは出てこないと思います。
そこで使うのが「たすきがけ」です!

詳しく解説すると少し長くなるため別記事で解説しようと思います!
出来次第下にリンク貼りますね( ^ω^ )
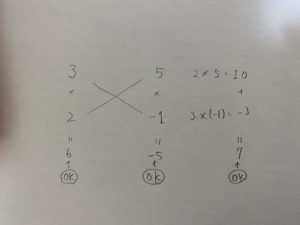

字ちっさ!んで汚い!

すみません今後改善します(´;Д;`)
ということで
6x²+7x−5=(3x+5)(2x−1)
となります。

問題演習…の予定でしたが
当初は問題演習も本記事に組み込む予定でしたが、予想以上に基礎部分が厚くなってしまったため、別記事でやろうかと思います。

因数分解は難しい問題はほんとに解くのに苦労します。
一言アドバイス。因数分解はとにかくたくさんの問題を解くことが一番上達します。
公式を何度も見て書いて覚えるよりかは、公式を見ながらでもいいのでじゃんじゃん演習をした方がいい気がします。そのうち公式が身につきつつ、問題を眺めると解法のパターンが出てくるようになるでしょう。

これはあくまで個人的な意見です。違うと思ったら他の方法で実力をつけていって頂けたらいいと思います( ^ω^ )
頑張ってくださいね!



