【高校数A】整数の性質「最大公約数」「最小公倍数」を元数学科が解説

今回は『最大公約数』『最小公倍数』を学習します。

 

「倍数」と「約数」について。

本題に入る前に復習しましょう。

実はこれ、前の記事で書いてありますので貼っておきます(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

 

【高校数A】整数の性質「約数と倍数」「倍数の判定法」を元数学科が解説

今回は【高校数学】【数A】『整数の性質』から「約数と倍数」「倍数の判定方法」を解説しました。教科書だと３、４ページくらいで収まる内容を丁寧に解説してみましたので、数学が苦手な方はぜひご覧ください！約数、倍数の定義や倍数の判定方法の証明などなど…

www.zilleblog.com

2022.02.11

 

 

「公倍数」「公約数」について。

では倍数・約数に漢字の「公」がついた「公倍数」「公約数」とはなんだろう？

ズバリ

です！

 

『公約数・公倍数の求め方』

試しに１２と１８の公約数を求めてみましょう٩( ‘ω’ )و

 

 

「最大公約数」「最小公倍数」について。

とうとう本題です。

意味はそのままで

 

 

 

 

実践問題を解いてみよう！

基礎を学んだところで次にテストで出題される難易度の問題を解説します。

 

 

問１：１０８と３６０の最大公約数と最大公倍数を求めなさい。

先ほど１２と１８で求めた問題の難しいバージョンです。

１２や１８のような小さい数ならすぐに求められるのが、３桁以上になると一気に分からなくなります(；ω；)

じっくり解説していきますねψ(｀∇´)ψ

手順①：２つの数をそれぞれ素因数分解する。

【高校数A】整数の性質「素数と素因数分解」を元数学科が解説

今回は【高校数学】【数A】『整数の性質』から「素数」「素因数分解」を解説しました。そもそも素数とは何かを解説して、素因数分解を手順を追って解説、最後に頻出問題を丁寧に解説してありますのでぜひご覧ください。

www.zilleblog.com

2022.03.13

 

まずは１０８を素因数分解してみましょう。

つまり$108=2^2\times 3^3$

次に３６０を素因数分解します。

つまり$360=2^3\times 3^2\times 5$

 

手順②：最大公約数を求める。

では最大公約数から求めましょう。

手順①で導き出した２つの因数分解を並べます。

$108=2^2\times 3^3$
$360=2^3\times 3^2\times 5$

$108=2^2\times 3^3\times 5^0$
$360=2^3\times 3^2\times 5^1$

注目するのは各素数の右上の数字”指数”です。

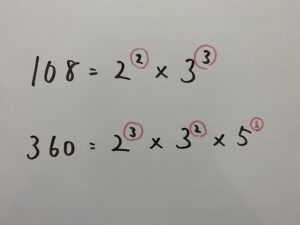
そしてここ大事。最大公約数は、それぞれの素数の指数を比べて小さい数字を取り上げます。

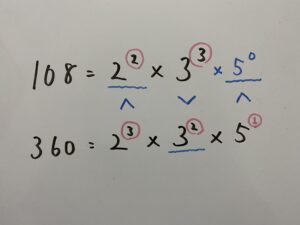
それらを掛けたものが最大公約数になります。

$2^2\times 3^2\times 5^0=4\times 9\times 1=36$

答えは36。

 

手順③：最小公倍数を求める。

こちらも最大公約数の求め方と似ています。

まずは108と360の素因数分解を並べましょう。

$108=2^2\times 3^3\times 5^0$
$360=2^3\times 3^2\times 5^1$

最小公倍数は、それぞれの素数の指数を比べて大きい数字を取り上げます。

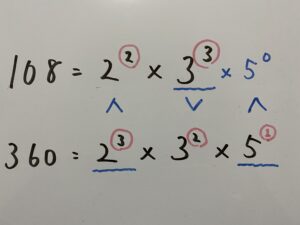
それらを掛けたのが最小公倍数です。

$2^3\times 3^3\times 5^1=8\times 27\times 5=1080$

答えは1080。

 

問１の答え

$108=2^2\times 3^3$
$360=2^3\times 3^2\times 5$

よって最大公約数は$2^2\times 3^2=36$

最小公倍数は$2^3\times 3^3\times 5=1080$

 

研究：なぜ最大公約数と最小公倍数は②，③の方法で求められるのか？

学校の教科書にはこれ以上の説明がありませんが今回もう少し掘り下げてみます。

なぜ上の方法で求められるのかです。

 

【最大公約数について】

まずは１０８について、その約数を全て書き出してみましょう。

１,２,３,４,６,９,１２,１８,２７,３６,５４,１０８

です。

これらの約数は

$108=2^2\times 3^3$

から

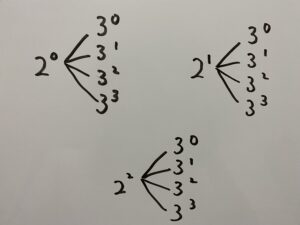
と表を作り、各場合で掛け算をすると

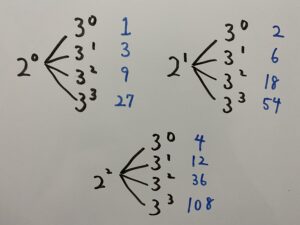
一致した！！！

まあ当たり前なことですが、ここで改めて認識しておいて欲しかったのです。

３６０でも同じように

$360=2^3\times 3^2\times 5$

表を書くと

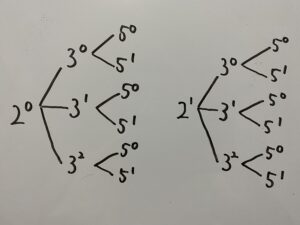
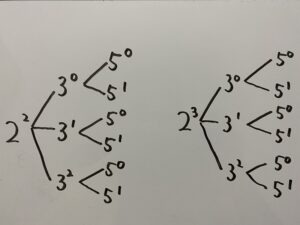
各場合の掛け算をすると

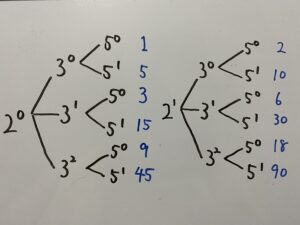
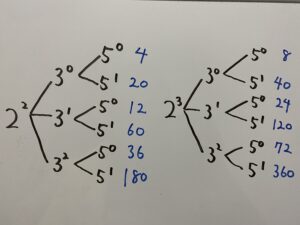
これらが３６０の約数です。

 

ここまで分かったら次は１０８と３６０との最大公約数を考察しましょう。

 

１０８の約数は２、３の累乗の掛け算、３６０の約数は２、３、５の累乗の掛け算であることが分かりますね？

なので

$2^x\times 3^y\times 5^z$

を考えてみましょう。（x,y,zは０以上の整数）

まずxについて

$x\geqq 3$の場合、$2^x\times 3^y\times 5^z$は360の約数にはy,zの数字によってはなり得ますが108の約数にはなり得ません。

$0\leqq x\leqq 2$であればy,zの数によっては108と360の公約数になり得るわけです。

 

yについても

 

$y\geqq 3$だと360の約数ではなくなります。

$z=0$ならx,yの数によっては108と360の約数となり得ます。

 

以上をまとめますと、$2^x\times 3^y\times 5^z$がが108と360の公約数となるには

$0\leqq x\leqq 2$かつ$0\leqq y\leqq 2$かつ$z=0$

です。

今回求めるのは最大（の）公約数ですよね？

考えてみましょう。$2^x\times 3^y\times 5^z$において、x,y,z,が大きいほどその数は大きくなりますよね？

よって最大公約数は、x,y,zそれぞれの最大値をとればいいのです！

$0\leqq x\leqq 2$かつ$0\leqq y\leqq 2$かつ$z=0$

の範囲でx,y,zの最大値はx=2,y=2,z=0です。

$2^2\times 3^2\times 5^0=36$

したがって108と360の最大公約数は36であると分かるわけです。

 

【最小公倍数について】

次に最小公倍数の求め方を詳しく解説します。

$108=2^2\times 3^3$

であることから、

$2^2\times 3^3\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数})$

は全て108の倍数になることは分かりますか？

 

同じように360についても

$360=2^3\times 3^2\times 5$より

$2^3\times 3^2\times 5\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数})$

は360の倍数になります。

 

今回は108と360の最小（の）公倍数を求めるので

$2^2\times 3^3\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数}A)$←108の倍数
$2^3\times 3^2\times 5\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数}B)$←360の倍数

最小の公倍数になるようにA,Bにふさわしい自然数を見つけましょう。

もう少し砕けた言い方をすると、

108と360それぞれにできるだけ小さな自然数を掛けて同じ自然数にしようってことです。

$2^2\times 3^3\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数}A)$←108の倍数
$2^3\times 3^2\times 5\times (\mathrm{何}\mathrm{か}\mathrm{し}\mathrm{ら}\mathrm{の}\mathrm{自}\mathrm{然}\mathrm{数}B)$←360の倍数

ここでやることが各素数の指数を比べて大きい方に合わせることです。

どういうことかと言いますと、

《2の指数》
108の素因数分解では2の素数は2、360の素因数分解では2の素数は3。よって3に合わせます。つまり108に2を1つ分掛けます。

$2^2\times 3^3\times (2)$
$2^3\times 3^2\times 5$

《3の指数》

108の素因数分解では3の素数は3、360の素因数分解では3の素数は2。よって3に合わせます。つまり360に3を1つ分掛けます。

$2^2\times 3^3\times (2)$
$2^3\times 3^2\times 5\times (3)$

《5の指数》

108の素因数分解では5の素数は0、360の素因数分解では5の素数は1。よって1に合わせます。つまり360に3を1つ分掛けます。

$2^2\times 3^3\times (2\times 5)$
$2^3\times 3^2\times 5\times (3)$

すると

$2^2\times 3^3\times (2\times 5)=2^3\times 3^3\times 5=1080$
$2^3\times 3^2\times 5\times (3)=2^3\times 3^3\times 5=1080$

 

これで、それぞれできるだけ小さい自然数を掛けて最小（の）公倍数が出ました！

 

まとめ