みなさんおはこんばんにちは！
暖かくなったと思ったら寒くなったりで困惑するジルでございます！
「因数分解が上手くいかない。」
「複雑なタイプの因数分解の解き方がわからない。」
「因数分解のマニュアルがあれば欲しい。」
こういった方結構いるのではないでしょうか。
今回は私ジル（元数学科）が因数分解を解く際に考えていることを公開したいと思います。
今回は二次式の因数分解です。
因数分解をする際考えていること
一般的な因数分解は
$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$
で表せられます。
これを元に解説します。
①acの組み合わせを考える。
②bdの組み合わせを考える。
③ad+bcの組み合わせを必死こいて考える。
こんな感じです。
理由は、まずはac、ad+bc、bdの中でacが簡単になりがちなのでまずはそこを攻めます。その後bdを攻めます。ac、bdのパターンを先にピックアップしておかないとad+bcはまずわからないでしょう。
とはいえ問題によってはacあるいはbdのパターンがかなり多い場合もあります。その場合はad+bcを見つけるのは結構大変ですががんばりましょう！
なんかね、問題の数をこなすと少しずつ「あ、この組み合わせ辺り怪しい」とかわかってきますよ！
練習問題解いてみる！
いくつか問題を解いてみましょう！たくさん問題を解くことで上達しますからね(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
（１）$8x^2+2x-15$
先程の$acx^2+(ad+bc)x+bd=(ax+b)(cx+d)に当てはめてみると
ac=8、ad+bc=2、bd=-15になります。
①acの組み合わせを考える
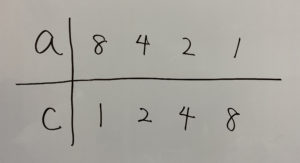
ここで鋭い方は
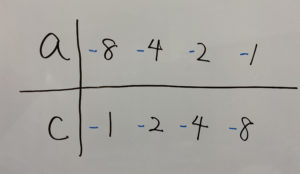
この場合もあるのでは？と気づくのではないでしょうか？今回は考えなくても良いのです。理由は後で説明します。
②bdの組み合わせを考える
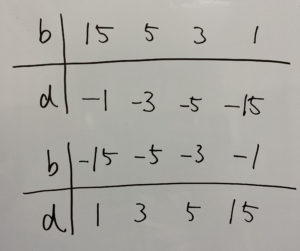
こんなですね。
③ad+bcの組み合わせを必死こいて考える
からad+bc=2になるパターンを探します。
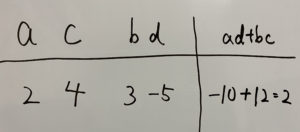
したがって
$8x^2+2x-15=(2x+3)(4x-5)$
ちなみに先程の
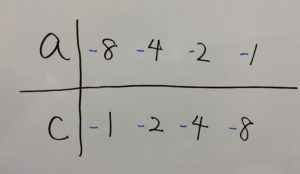
のパターンの話ですが、これも入れると
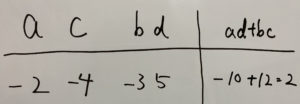
の組み合わせもあります。しかしこの場合
$(-2x-3)(-4x+5)=\{-(2x+3)\}\{-(4x-5)\}=(2x+3)(4x-5)$
と結局同じになるんですよねー。
（２）$3x^2-2xy-8y^2$
さて同じ要領で解きましょう。
①acの組み合わせを考える
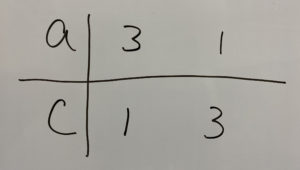
②bdの組み合わせを考える
③ad+bcの組み合わせを必死こいて考える
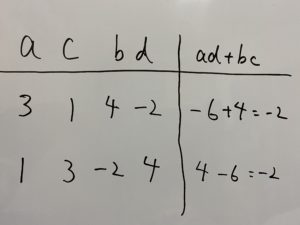
したがって
$3x^2-2xy-8y^2=(3x+4y)(x-2y)$
または
$3x^2-2xy-8y^2=(x-2y)(3x+4y)$
ところがこの２つは同じなので、どちらか１つの答えを書けばオッケーです。
（３）x^2-3xy+2x+2y^2-5y-3$
こういう複雑な問題は１つ工夫をしましょう。それは
『１つの文字に注目してその文字について降べきの順に並べる』
ことです。
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
今回はxについて降べきの順に並べて考えましょう。
$x^2-(3y-2)x+(2y^2-5y-3)$
この後は今までやってきた手順でいけます。
①acの組み合わせを考える
これは1と1の組み合わせのみです。
②bdの組み合わせを考える
（１）、（２）と違ってこの手順で一手間必要です。
$2y^2-5y-3$のままでは組み合わせを考えづらいですね？
ここで因数分解できるか考えます。
この程度の因数分解はたすきがけを使えば余裕ですね？
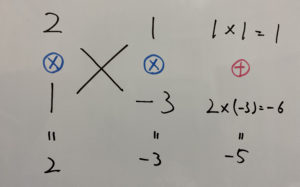
したがって$2y^2-5y-3=(2y+1)(y-3)$
したがって組み合わせは$2y+1$と$y-3$になります。
③ad+bdの組み合わせを必死こいて考える
今回は必死こいて考える必要はありません（ﾎｯ…）
①も②も組み合わせは１通りしかなかったですから！
いちお確認してみましょう。
したがって
$x^2-(3y-2)x+(2y^2-5y-3)=x^2-(3y-2)x+(2y+1)(y-3)$
$=\{x-(2y+1)\}\{x-(y-3)\}=(x-2y-1)(x-y+3)$
最後に
今後もみなさんが特につまづきそうなポイントを解説したいと思います！
楽しい数学Lifeを！
