
みなさんこんばんは、ジルでございます!
因数分解は楽しめていますか?笑
私ジルは因数分解大好きですよ( ̄▽ ̄)
複雑な問題が因数分解されてキレイな式に直されるのがたまりません!
さて、最近は数学ジャンルの記事は因数分解のことばかり書いていますが今回が最後になります。
今回は…
少し難しめの問題にチャレンジしたいと思います!
「比較的出題されそうな難しい」レベルの問題を解説したいと思います。
今回の問題
(1)6x²+10xy−4y²+7x+7y+2
(2)a²−4a−4b²+4
(3)x⁴+4
このレベルになってくると、経験がモノをいいます。
一生懸命たくさん問題を解いた人が有利になります。

さあ、一緒に見ていこう!
解答
今回も私が因数分解を解く際のステップを用います。
①問題をじっくり眺める。
②共通項があれば、ab+ac=a(b+c)のようにしてまとめる。
③a²+2ab+b²=(a+b)²
a²−b²=(a+b)(a−b)
の公式が使えるかチェックする。使えれば使って、使えなければ④へ。
④acx²+(ad+bc)+bd=(ax+b)(cx+d) a,b,c,dは定数
を使って解く。
(1)6x²+10xy−4y²+7x+7y+2
考え方
①問題をじっくり眺めます。
②見た感じ共通項はなさそうです。
③いかにも公式は使えなさそうです。
④因数分解が苦手な方、まだ勉強し始めて間もない方はこう思うでしょう。

これ解くの無理じゃね?よし、飛ばそう。

逃げちゃダメだ逃げちゃダメだ…。
確かにテストにおいてはパッと見ムズそうな問題は一旦飛ばすのは有効策ではあります。
ただこういう問題、やり方知っておくと結構解けます。いいカモっすよ笑。
まずやることは
『ある文字について、降べきの順に並べること』
です。

降べきの順がわからない方は教科書やネットで調べてみて!すぐ出るよ!
今回の問題ではxとyの文字が使われています。どちらの文字で降べきの順に並べても最終的に同じ答えになります。
せっかくなので両方の文字で試してみますね!
xについて降べきの順に並び替える。
6x²+10xy+7x−4y²+7y+2
こうなります。次に同じ次数をカッコでまとめます。
6x²+(10y+7)x−(4y²−7y−2)
6x²…次数は2 (10y+7)x…次数は1 −(4y²−7y−2)…次数は0
にできますね?

カッコの前にマイナスがある場合の符号に気をつけてね!
次に考えるのが、
「次数が0の部分が因数分解できないかを見る」
です。見てみましょう。
まずカッコの前にあるマイナスは後でつければ良いので無視します。
4y²−7y−2
について
①問題をじっくり眺める。
②共通項はなさそう。
③公式は使えなさそう。
④たすきがけで考えてみましょう。すると
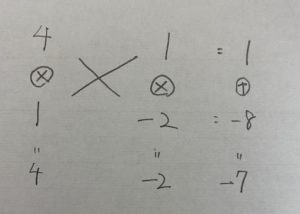
よって
4y²−7y−2=(4y+1)(y−2)
となります。つまり 6x²+(10y+7)x−(4y²−7y−2) の部分は
6x²+(10y+7)x−(4y−1)(y−2)
と表すことができるんです!
さあ次にやることは
この式をたすきがけで解く
です。

え、いつもは数字だけなのに今回は文字のy入ってますやん…。
無理ですやん…。
そんなことないです!
意外と簡単にできます。なぜなら
acx²+(ad+bc)x+bd=(ax+b)(cx+d)
について解き方を
❶acの組み合わせを考える。
❷bdの組み合わせを考える。 etc…
と教えましたが、bdの組み合わせは
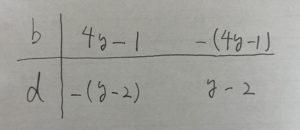
だけで良いからです。
ではたすきがけをしていきましょう!
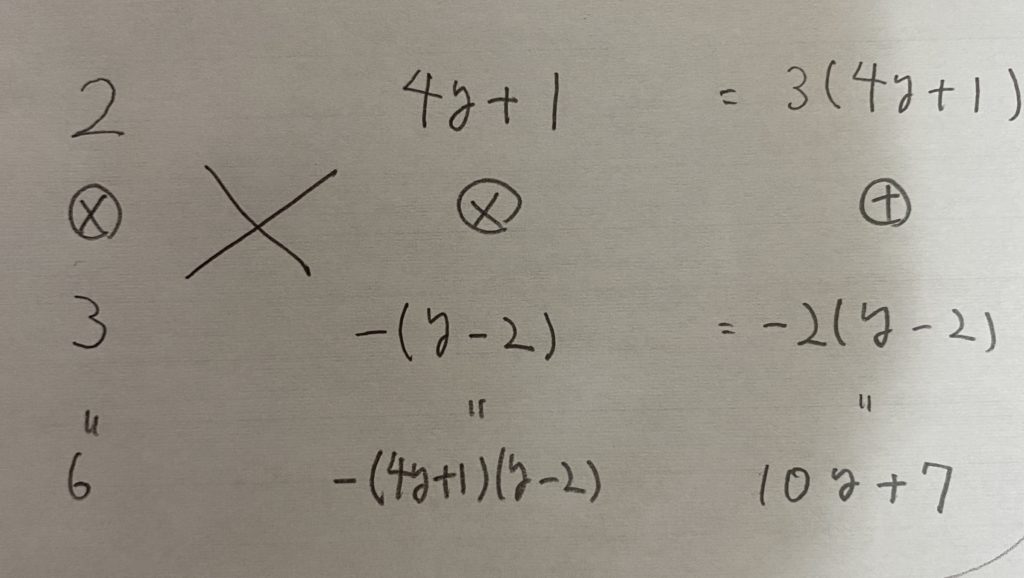
したがって、
6x²+(10y+7)x−(4y−1)(y−2)={2x+(4y+1)}{3x−(y−2)}=(2x+4y+1)(3x−y+2)
以上から、
6x²+10xy−4y²+7x+7y+2=(2x+4y+1)(3x−y+2) 終
yについて降べきの順に並び替える。
次はyに注目した場合で解いてみましょう。並び替えると
−4y²+10xy+7y+6x²+7x+2
次に同じ次数をカッコでまとめます。
−4y²+(10x+7)y+(6x²+7x+2)
さあ次は次数が0の部分を因数分解しましょう。
6x²+7x+2について
①問題をじっくり眺めましょう。
②共通項はなさそうです。
③パッと見公式は使えなさそう。
④すぐには解けそうにありません。たすきがけを使いましょう!
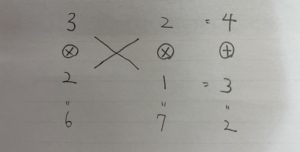
よって
6x²+7x+2=(3x+2)(2x+1)
したがって
−4y²+(10x+7)y+(6x²+7x+2)=−4y²+(10x+7)y+(3x+2)(2x+1)
次はこの式を因数分解します。たすきがけを使うとできますね!
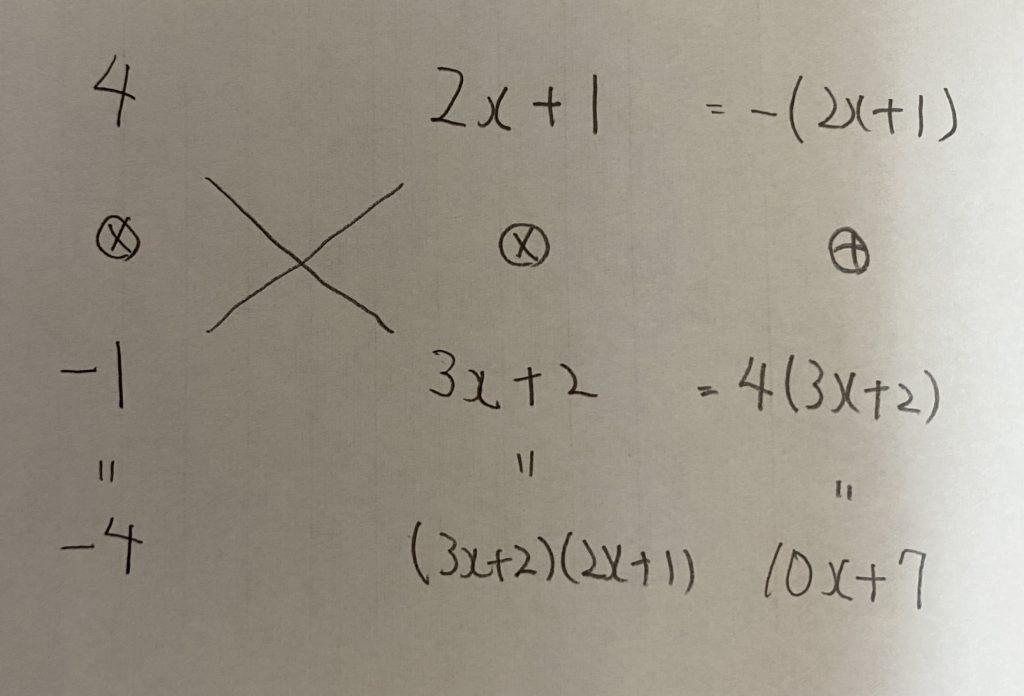
したがって
−4y²+(10x+7)y+(6x²+7x+2)={4y+(2x+1)}{−y+(3x+2)}=(2x+4y+1)(3x−y+2) 終
両方の場合で試しましたが結局同じになりましたね!
下に、改めて解答をまとめますね。
解答
6x²+10xy−4y²+7x+7y+2=6x²+(10y+7)x−(4y²−7y−2)
=6x²+(10y+7)x−(4y−1)(y−2)
={2x+(4y+1)}{3x−(y−2)}
=(2x+4y−1)(3x−y+2)
(2)a²−4a−4b²+4
さてコチラの問題。(1)に比べると複雑には見えませんね?
ただ初見さんが挑むと割と手が止まってしまいがちです。
一緒に解いてこのパターンも身につけましょう!
考え方
①じっくり問題を眺めます。
②共通項はなさそうです。
③公式は使えなさそうです。
④うーん、パッと見すぐにはたすきがけできなさそうです(ㆀ˘・з・˘)
ではどうやって解きましょうか?
先に結論言っておきます。
解き方1:(1)のように降べきの順に整理してから解く。
解き方2:実は③の公式が使える形にできる。
です。
本記事はじっくり問題を解説するスタンスで書いておりますので両方やってみますね!
解き方1
こちらは(1)と同じ手順で解いておりますので、少し省略して書きます。
わからなくなったら(1)の考え方をもう一度見てみてください。
aについて降べきの順に並べてみましょう。
a²−4a−(4b²−4)
ですね。さて次は「次数0の部分が因数分解できないか考える」です。
4b²−4について
①じっくり問題を眺めます。
②項全てが4の倍数ですね?よって共通項は4です。よって
4b²−4=4(b²−1)
にできます。なのでカッコの中を因数分解すれば良くなりました!
③もうこの応用編の記事を読んでいるみなさんはすぐにわかりますね?
b²−1=(b+1)(b−1)
したがって
a²−4a−(4b²−4)=a²−4a−4(b+1)(b−1)
はいここまできました。次はコチラの式を因数分解します。
①問題をじっくり眺めます。
②共通項はなさそうです。
③パッと見公式は使えなさそうです。
④たすきがけしましょう。

文字が絡んでる因数分解は大抵たすきがけを使いますね。
答えのたすきがけをやってみると
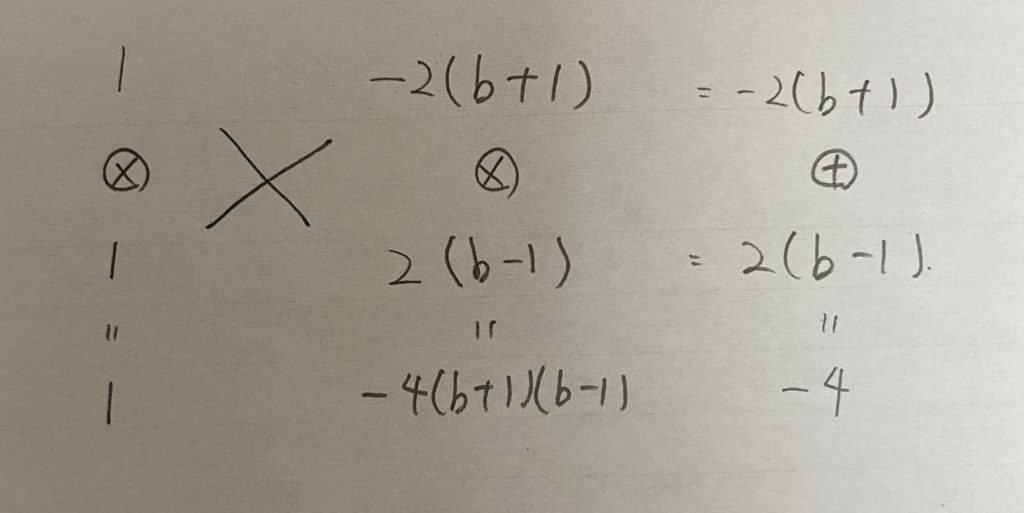
となります。4(b+1)(b−1)を2(b+1)×2(b−1)と考えるのがミソですね!
したがって、
a²−4a−4b²+4=a²−4a−4(b+1)(b−1)={a−2(b+1)}{a+2(b−1)}
=(a+2b+2)(a−2b+2) 終
解き方2
コチラの解き方は少しひらめきが必要になりますが、解き方1よりかなり楽に解けます。
模範解答はコチラです。
実際に解き方を見て頂いた方がいいと思うので書きますね!
a²−4a−4b²+4=a²−4a+4−4b²=(a−2)²−4b²={(a−2)+2b}{(a−2)−2b}
=(a+2b−2)(a−2b−2) 終
これだけです。③の公式が上手いこと使える問題ですね。
色の部分がしっかり頭に浮かんでくるかどうか…。
たくさん問題を解きましょう!すればこういうひらめきも出やすくなります。
解答
a²−4a−4b²+4=a²−4a+4−4b²=(a−2)²−4b²={(a−2)+2b}{(a−2)−2b}
=(a+2b−2)(a−2b−2) 終
(3)x⁴+4
すごく短い問題!でもこういう問題ほど手こずったりするんですよねこれが!
あと4乗っていうのもミソです。
こういう問題はひらめくしかないです。まずは、次のような変形が浮かぶかが重要です。
x⁴+4=(x²−2)²−4x²
ここまでこればわかりますかね?そう、(2)の解き方2と同じような考え方です!

a²−b²=(a+b)(a−b)ですね。みなさんもう完璧ですか?
では解答をしましょう。
解答
x⁴+4=(x²−2)²−4x²={(x²−2)+2x}{(x²−2)−2x}=(x²+2x−2)(x²−2x−2)
最後に
今記事では「複雑に入り組んでいる問題への考え方」「解法をひらめかないと厳しい問題」を解説してきました。
しかしこういう問題を見たことがない方は正直解くのは困難ですね。

天才型の方は別ですが笑
たくさん問題を解きましょう。因数分解の全記事で口酸っぱくして言っていますが笑。
私ね、数学苦手な人って問題解く量増やせばなんとでもなると思うんですよ。
私は一応数学は得意で大学数学科卒まで至りました。
でも私別に才能あるわけでもないと思うんです。
実際大学生の時数学科の先輩から「〇〇って数学のセンスはないよね笑。」って言われました( ̄▽ ̄)
ただね、いっぱい問題解いたんです。だからここまで来れたと思っています。

努力は実ります。頑張りましょう!



