【高校数A】整数の性質「約数と倍数」「倍数の判定法」を元数学科が解説

最近までずっと図形について学んできましたがここからはまた分野が変わりまして、整数について掘り下げていきます。

本題に入る前に…実数、虚数、有理数、無理数、整数、分数、自然数について

みなさん『数』にはいろんな種類があるのご存知ですか？

高校数学まででも相当な種類が出てきております。ここらで一度整理してみましょう！

それぞれの分岐を解説します。

「実数」と「虚数」

これまで習ってきた数は全て「実数」になります。

高一のみなさんは今は気にしなくてもオッケーです！

 

「有理数」と「無理数」

有理数については中学数学で習っているはずです。

 

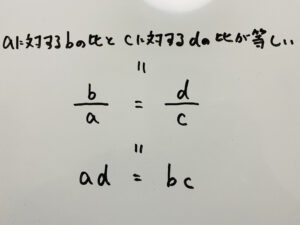
「整数」と「分数」

まあこちらは説明せずとも分かりますよね。

 

「正の数」と「０」と「負の数」

整数とは

…,-3,-2,-1,0,1,2,3,…

こんな数ですね？

これを「正の数」「０」「負の数」に分けてみましょう。

…,-3,-2,-1,0,1,2,3,…

 

 

「約数」「倍数」とは？

整数についてもう少し掘り下げていきます。

…,-3,-2,-1,0,1,2,3,…

a、bを整数とします。

この時

$a=bk(kはある整数)$

と表される時

aはbの倍数である

といい、

bはaの約数である

と言う。

例）８の約数を求めなさい。

まずは先程出した約数の定義より

$8=b \times k(kはある整数)$

で表せる時のbを求めれば良いんです！

早速書き出してみましょう。

したがって答えは1,2,4,8  …ではありません！！！！

整数の定義を思い出して下さい。

…,-3,-2,-1,0,1,2,3,…

大事なのはマイナスも含まれているってこと！

つまりですね、先程書き出した表に

こうやってマイナス分も書き出せるわけよ！

したがって正しい答えは

1,2,4,8,-1,-2,-4,-8

です。

 

例）３の倍数は？

先ほど出した倍数の定義より

$a=3 \times k(kはある整数)$

を満たすaを求めれば良いです。

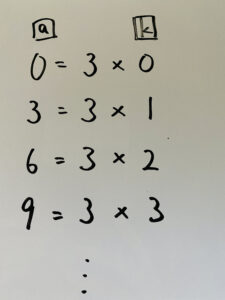
つまりa=0,3,6,9,…   ではないですからね！！！！

先ほども申しました通り整数とは

…,-3,-2,-1,0,1,2,3,…

とマイナスも含まれています。

つまり

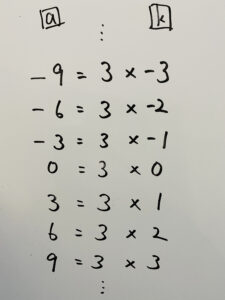
も書き出せるわけですわ（＾∇＾）

したがって

a=…,-9,-6,-3,0,3,6,9,…

 

基本的な証明問題を１つ

問：a,bを整数とする。a,a+bが６の倍数ならば、bが６の倍数であることを証明しなさい。

（証明開始）

まずは約数、倍数の定義より

aが６の倍数→$a=6p(pは整数)$

a+bが6の倍数→$a+b=6q(qは整数)$

と表せます。

ここで注意が１つ！

aが６の倍数→$a=6p(pは整数)$

a+bが6の倍数→$a+b=6p(pは整数)$

としないように！

 

aが６の倍数→$a=6p(pは整数)$…①

a+bが6の倍数→$a+b=6q(qは整数)$…②

①を②に代入して

$6p+b=6q$

移行して

$b=6q-6p=6(q-p)$

p,qが整数なのでq-pも整数です。

これでbが6の倍数であることが分かります。

（証明終了）

 

倍数の判定法（色々あります）

次は自然数のお話。

みなさん、ある自然数がなんの倍数か調べるにはどうしたら良いか分かりますか？

ただし全ての数に判定方法があるわけではありません。今回は2,3,4,5,8,9の判定方法を解説します！

早速見ていきましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

ではそれぞれ判定方法について、なぜその方法で分かるのかを証明します！！！

２の倍数：一の位の数が0,2,4,6,8のいずれか

これは証明するまでもないですね。

一の位の数が0,2,4,6,8のいずれかということはその数は偶数です。

偶数は２で割れるのは当然なので！

 

３の倍数：各位の合計が３の倍数

まずは判定方法の証明において大切な考え方をお伝えしておきます。

といってもそんなに長いものでもなく

$92=2 + 9 \times 10$

$124=4 + 2 \times 10 + 1 \times 100$

と表せるってものです。これから証明するほとんどにこれが利用されるので覚えといて！

 

（証明開始）

自然数について、

$a+10b+100c+1000d+…$

a：一の位の数
b：十の位の数
c：百の位の数
d：千の位の数

どんな自然数もこの形で表せます。

ここで１つ、

$10b-b=9b=3 \times 3b$
$100c-c=99c=3 \times 33c$
$1000d-d=999d=3 \times 333d$

この考え方が大事

$a+10b+100c+1000d+…=a+(9b+b)+(99c+c)+(999d+d)$
$=(9b+99c+999d+…)+(a+b+c+d+…)$
$=3(3b+33c+333d+…)+(a+b+c+d+…)$

と表せます。

$3(3b+33c+333d+…)$は３の倍数です。

$a+b+c+d+…$について、こちらは各位の数の和であることはみなさん分かりますか？？分かりますよね？？

 

ではここで皆さんに問題です。

$3(3b+33c+333d+…)+(a+b+c+d+…)$

が３の倍数になる条件は何でしょうか？？

 

なぜかと言いますと、$a+b+c+d+…$が３の倍数と仮定すると、

$a+b+c+d+…=3V（Vは整数）$

と置き換えることができます。すると

$3(3b+33c+333d+…)+(a+b+c+d+…)=3(3b+33c+333d+…)+3V$

$=3(3b+33c+333d+…+V)$

つまり３の倍数であることが分かりますね？

 

先程申し上げた通り$a+b+c+d+…$は「各位の数の和」ですから

$a+b+c+d+…$が３の倍数→その自然数は３の倍数

したがって

各位の数の和が３の倍数→その自然数は３の倍数

（証明終了）

 

４の倍数：下２桁が４の倍数

例）34232は下２桁が３２、３２は４の倍数なので３４２３２は４の倍数

こういうことですね。

なぜそうなるのかをまた証明します！

（証明開始）

ある自然数について

$a+10b+100c+1000d+…$

と表現します。

ここで１つ、

$100c=4 \times 25c$

$1000d=4 \times 250d$

などなど…100,1000,10000,…は全て４の倍数であることを覚えておいて下さい。

したがって

$a+10b+100c+1000d+…=(a+10b)+4(25c+250d+…)$

と表せます。

 

ここでみなさんに問題です。

$(a+10b)+4(25c+250d+…)$

が４の倍数になる条件は何でしょうか？？

 

なぜかと言いますと

a+10bが４の倍数と仮定すると、整数Vを用いて

$a+10b=4V$

と表すことができます。すると

$a+10b+4(25c+250d+…)=4V+4(25c+250d+…)=4(V+25c+250d+…)$

したがって４の倍数となります。

a+10bは自然数の下２桁の部分になることはみなさん分かりますか？

したがって自然数が４の倍数になる条件は下２桁が４の倍数であることが証明されました。

（証明完了）

 

５の倍数：一の位が０か５

これみなさん分かりますかね？

５の倍数って5,10,15,20,…と一の位が０と５の繰り返しですよね。

 

一応証明しておきますか！

（証明開始）

ある自然数について

$a+10b+100c+1000d+…$

a：一の位の数
b：十の位の数
c：百の位の数
d：千の位の数

と表します。

ここで注目すべきは

$10b=5 \times 2b$

$100c=5 \times 20c$

$1000d=5 \times 200d$

つまり

$a+10b+100c+1000d+…=a+5(2b+20c+200d+…)$

 

ではまたまたみなさんに問題です。

$a+5(2b+20c+200d+…)$

が５の倍数になる条件は何でしょうか？？

 

なぜならa=0の時

$a+10b+100c+1000d+…=5(2b+20c+200d+…)$

つまり５の倍数になります。

a=5の時

$a+10b+100c+1000d+…=5+5(2b+20c+200d+…)$
$=5(1+2b+20c+200d+…)$

つまり５の倍数になります。

aとは一の位の数ですので、したがって一の位が０または５の時、自然数は５の倍数になります。

（証明完了）

 

８の倍数：下３桁が８の倍数

こちらは正直イメージないですよね！でも成り立つんです！

（証明開始）

ある自然数を

$a+10b+100c+1000d+10000e+…$

a：一の位の数
b：十の位の数
c：百の位の数
d：千の位の数
e：万の位の数

ここで１つ、

$1000=8 \times 125$

$10000=8 \times 1250$

のように８の倍数になっているんです！つまり

$a+10b+100c+1000d+10000e+…=a+10b+100c+8 \times 125d+8 \times 1250e+…$
$=a+10b+100c+8(125d+1250e+…)$

ここでみなさんに問題です！（何回このやりとりやった？w）

$a+10b+100c+8(125d+1250e+…)$

が８の倍数になる条件はなんでしょうか？？

なぜかと言うと、$a+10b+100c$が８の倍数になるということは、自然数Vを用いて

$a+10b+100c=8V$

と置き換えられます。つまり

$a+10b+100c+8(125d+1250e+…)=8V+8(125d+1250e+…)$
$=8(V+125d+1250e+…)$

８の倍数になることが分かりますね(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

$a+10b+100c$が何を指しているかと言いますと、その自然数の下３桁です。

したがって、自然数の下３桁が８の倍数の時その自然数は８の倍数になることが証明されました。

（証明完了）

 

９の倍数：各位の合計が９の倍数

こちらは３の倍数の条件証明に似ています。

（証明開始）

自然数について

$a+10b+100c+1000d+10000e+…$

a：一の位の数
b：十の位の数
c：百の位の数
d：千の位の数
e：万の位の数

と表します。この式を次のように変換してみましょう。

$a+10b+100c+1000d+10000e+…$
$=(a+b+c+d+e+…)+(9b+99c+999d+9999e+…)$
$=(a+b+c+d+e+…)+9(b+11c+111d+1111e+…)$

 

ここでみなさんに問題です！（もう分かりますよね？）

$(a+b+c+d+e+…)+9(b+11c+111d+1111e+…)$

が９の倍数になる条件は何でしょうか？？

なぜなら、$a+b+c+d+e+…$が９の倍数と仮定すると、自然数Vを用いて

$a+b+c+d+e+…=9V$

と表せます。すると

$(a+b+c+d+e+…)+9(b+11c+111d+1111e+…)$
$=9V+9(b+11c+111d+1111e+…)$
$=9(V+b+11c+111d+1111e+…)$

つまり９の倍数になります。

（証明完了）

 

最後に（まとめ）