みなさんおはこんばんにちは。
少し寝不足で悩んでいるジルでございます！
今回は方程式の勉強です。ただしあまり聞き慣れない方程式です。
一次不定方程式です！
一次不定方程式とは？
この時
$ax+by=c$
を満たす(x,y)を求めることを一次不定方程式を解くという。
ん？ぱっと見ただの一次方程式を解くのと変わらないのでは？
１つの式に文字が２つあるってだけで。
確かに見た目はそんなに変化ないですね！具体例を出してみましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
$y=-\frac{2}{3}x+\frac{1}{3}$
$x=2$の時$y=-1$
$x=3$の時$y=-\frac{5}{3}$
中学とかで習った方程式って、解が１つとか２つとかそれくらいでしたよね？
今回みたいな文字が２つ含まれている方程式の場合、連立方程式を習ったのを覚えていますか？
$\begin{eqnarray} \left\{ \begin{array}{l} 2x + 3y = 1 \\ x + 5y = 3 \end{array} \right. \end{eqnarray}$
連立方程式なら解を１つに絞れます。
連立方程式の解き方覚えていますか？
忘れたこのために解いてみますね！
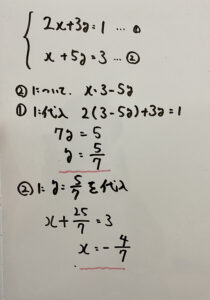
よって解は$(-\frac{4}{7},\frac{5}{7})$
頻出問題を解いてみる！
テストで出題されそうな問題をいくつか解いてみましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
$ax+by=1$を満たす解を1つ求めなさい。
ユークリッドの互除法を忘れたっていう子はこちらの記事をご覧ください。以前書いたユークリッドの互除法についての記事です！
$ax+by=1$の整数解を求めなさい。
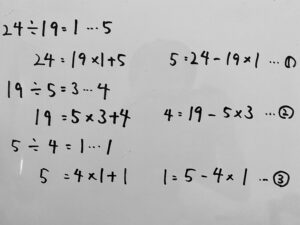
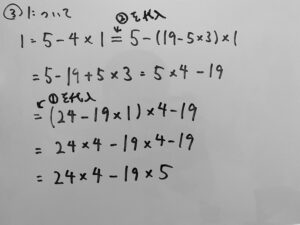
先ほどは具体的な解を１つ求めれば良かったのですが、今回は１つという指定がありません。
先ほど説明したように、一次不定方程式は解がいくつも存在します。
この場合は文字を使って解を表すのです！
これが解き方手順です。
実際にやってみましょう٩( ‘ω’ )و
$(元の式)：73x+55y=1$
$(①を代入した式)：73 \times (-3) +55 \times 4 =1$
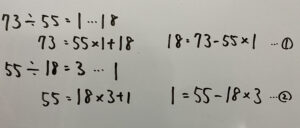
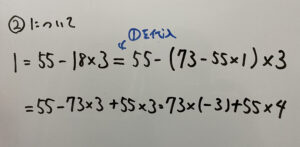
よって(元の式)-(①を代入した式)は
$(左辺)=(73x+55y)-\{73 \times (-3) +55 \times 4 \}=73(x+3)+55(y-4)$
$(右辺)=0$
③式を整理して文字を使って解を表す。
したがって
$73(x+3)+55(y-4)=0$が成立します。さらに移項して
$73(x+3)=-55(y-4)$
73と55は「互いに素」なので整数kを用いて
$x+3=-55k$、$y-4=73k$
と表すことができます。
なぜ「互いに素」ならこのように表せるのか分かりますか？これ数学が苦手な子は特に理解に苦しむかもしれないですね。
説明を下に捕捉しておくので分からない子は一度見てみてね( ^ω^ )
【「互いに素」についての補足事項】ーーーーーーーーーー
少し等式を簡略化しましょう。$x+3=m$、$n=y-4$と置いて
$73m=-55n$
73と55が「互いに素」とはどういうことだったでしょう？それは
公約数が１のみ
ってことです。そのことを踏まえて次のことを考えてみよう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
『約数と倍数』で勉強したことを覚えていますか？忘れた方はこちらの記事で復習してね！
つまり$73m=-55n$から
⑴73mは-55の倍数（-55は73mの約数）
⑵-55nは73の倍数（73は-55nの約数）
ということである。…ってことみなさん分かりますか？？
⑴について、73mが-55の倍数ということは73mを因数分解した時に-55が含まれているということです。
もし含まれていたら73と55の公約数が1だけであるわけがないからです。
73を因数分解した時に55が含まれていない以上、mに含まれているしかないのです。
あとはこれを$73m=-55n$に代入して
$73 \times (-55k)=-55n$
$n=73k$
あとはm、nを戻して
$x+3=-55k$
$y-4=73k$
ーーーーーーーーーーーーーーーーーーーーーーーーーーー
あとは移項すればok
$x=-55k-3$
$y=73k+4$
$ax+by=c$の整数解を全て求めなさい。
さっき紹介したパターンの右辺が1でないバージョンですね！
実際解き方もそんなに変わりません。
①$ax+by=1$をユークリッドの互除法を使って具体解を１つ求める。
$43x+18y=1$の具体解を１つ求めます。
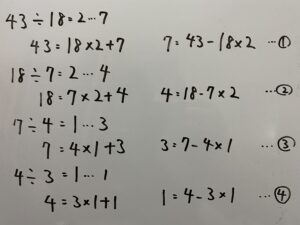
したがって$(x,y)=(-5,12)$が１つの具体解となります。
②具体解を$ax+by=1$に代入して両辺にcを掛ける。
$43 \times (-5)+18 \times 12=1$
両辺に5を掛けて
$43 \times (-5) \times 5+18 \times 12 \times 5=5$
$43 \times (-25) +18 \times 60=5$
③元の式から②の式を引く。
$43x+18y=5$
$43 \times (-25) +18 \times 60=5$
上の式から下の式を引くと
$(左辺)=(43x+18y)-\{43 \times (-25)+18 \times 60\}=43(x+25)+18(y-60)$
$(右辺)=0$
よって
$43(x+25)+18(y-60)=0$
移項して
$43(x+25)=-18(y-60)$
43と18は互いに素なので、ある整数をkとして$x+25=-18k$と表せます。
$x=-18k-25$
また$x+25=-18k$を$43(x+25)=-18(y-60)$に代入して
$43 \times (-18k)=-18(y-60)$
$-43k=-(y-60)$
$y=43k+60$
答えは
$x=-18k-25$
$y=43k+60$
最後に
結構文字が多くて苦手な人は少し嫌になるかもw
めげずに頑張ろう！理解できた時の達成感がたまりませんよ！
楽しい数学Lifeを！
