
みなさんおはこんばんにちは。
最近ニンニク食べすぎてどうにかなってしまいそうなジルでございます!
今回
『二項定理』
についての学習です。
前回記事にした三次式の展開・因数分解から続く内容ですのでもし不安な方はまずはこちらの記事からご覧ください(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

二項定理とは?
を展開する方法です。

これだけだと分かりづらいですが実は法則性があります。
・パスカルの三角形
・二項定理
のふたつの観点から見てみましょう!
パスカルの三角形
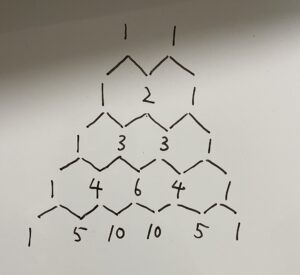
◎左右対象
◎左端、右端は常に1
◎左端、右端以外は左上と右上の数字の合計

勘のいい人は気が付いたでしょうか?
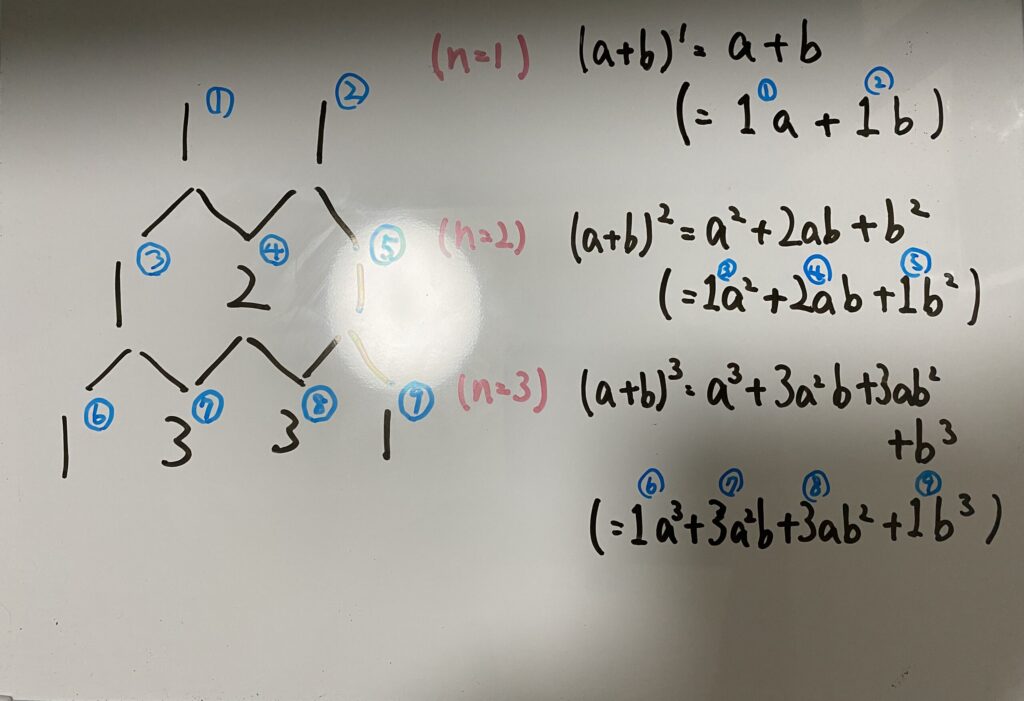
こういう法則になっているわけです。

ではみなさんn=4(4次式)
ぜひやってみてください。
答えは
です。分かりましたか??
二項定理
パスカルの三角形を使えばnの値がそんなに大きくなければ求められますが大きくなってきたら厳しくなってきます。そんな時使うのが『二項定理』になります。
ではいきます。

めっちゃムズそう!こりゃだめだ
やっぱり数学は嫌いだ!

とりあえず100回書いて覚えましょう。話はそれからです。
さきほど復習した
もこの定理に当てはまりますよ!
また二項定理
において
を一般項といいます。
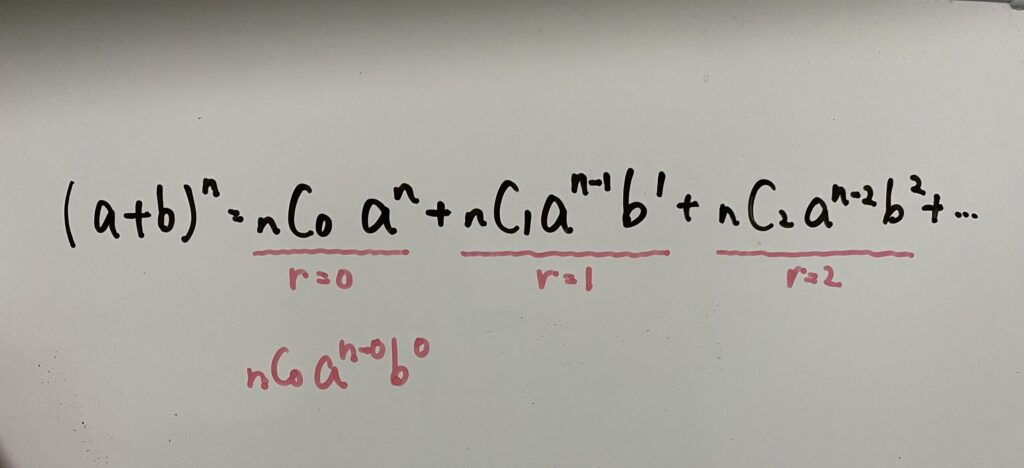
また
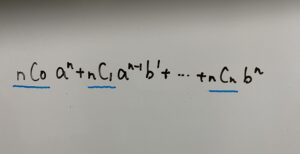
青線の部分を二項係数といいます。
練習問題①
次の式を展開しなさい。
(1)
(2)
(3)
(4)

二項定理で一番スタンダードな問題がこれですね。まずはここから完璧にしましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
解き方ですが、ただ二項定理の各文字に当てはめるだけです。
《解答》
(1)二項定理
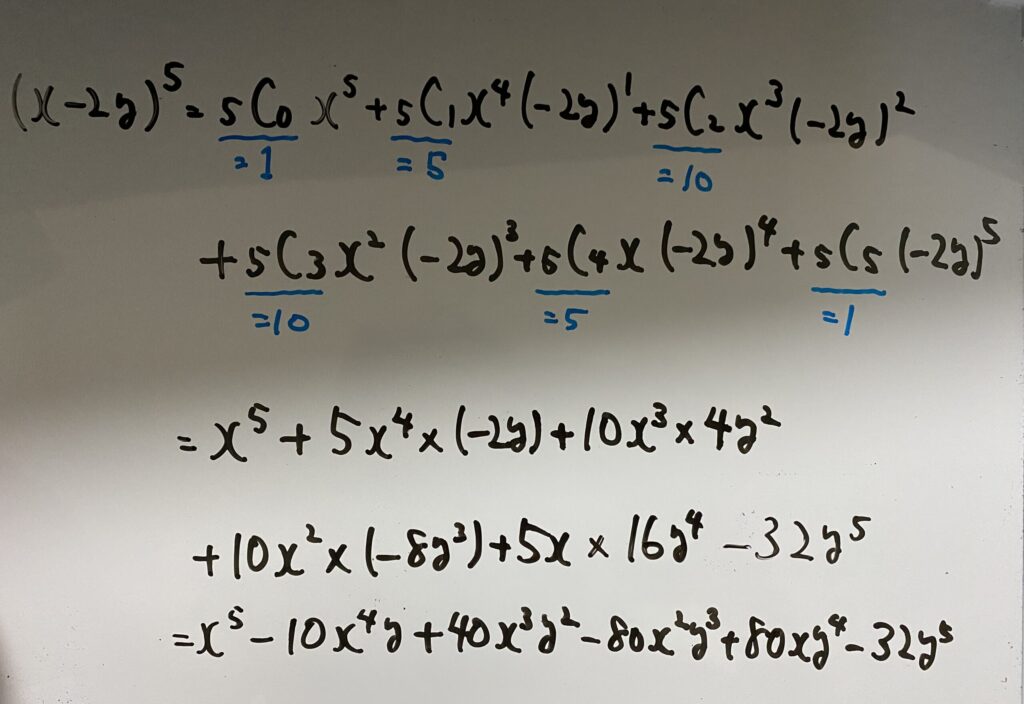
答え…
(2)二項定理
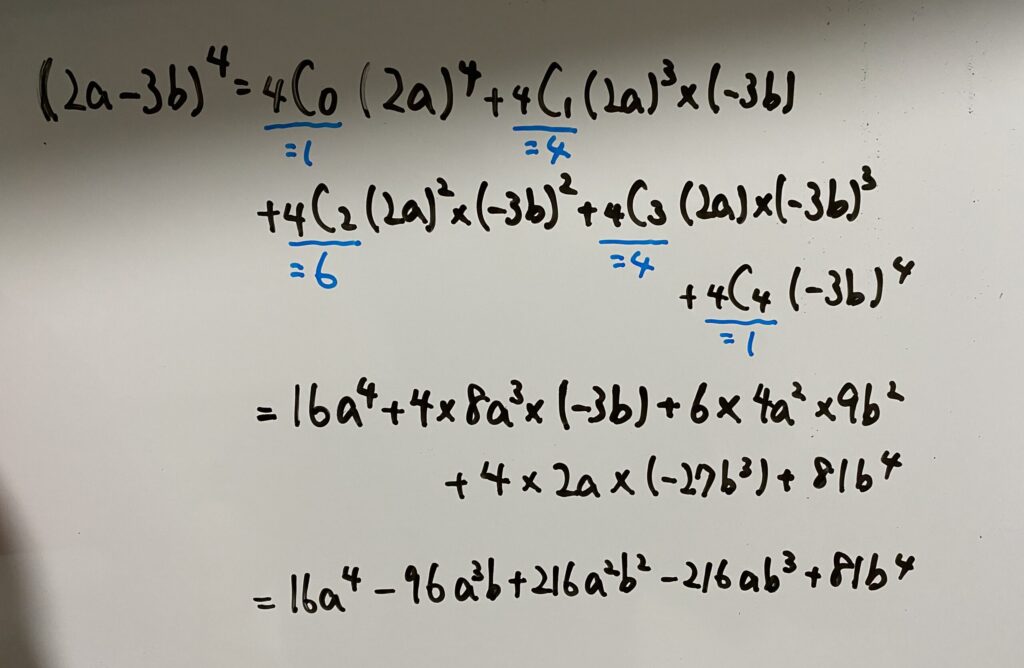
答え…
(3)二項定理
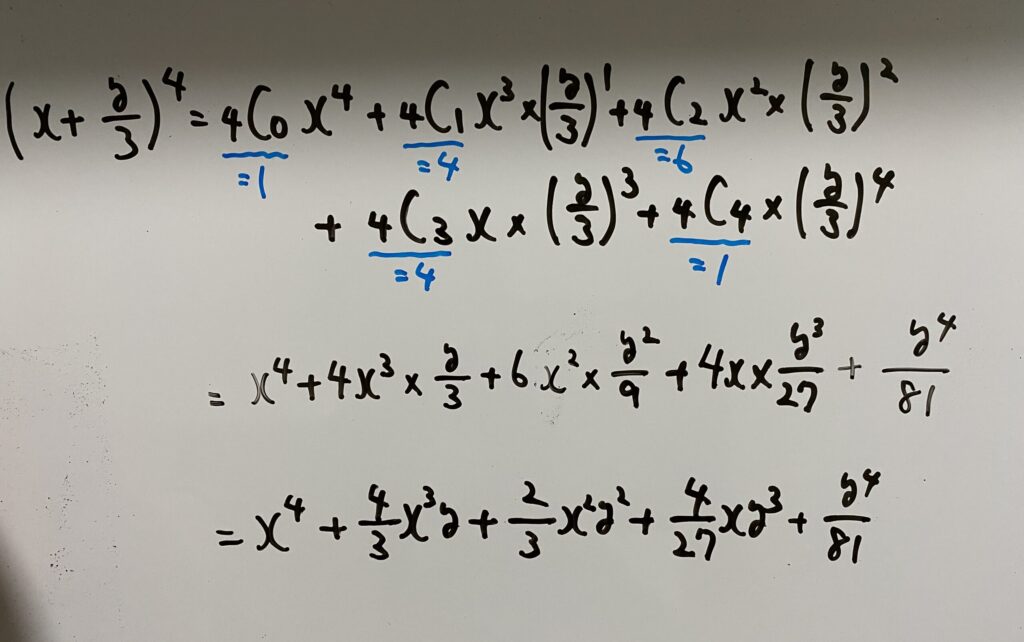
答え…
(4)二項定理

落ち着いて同じことをすれば大丈夫。
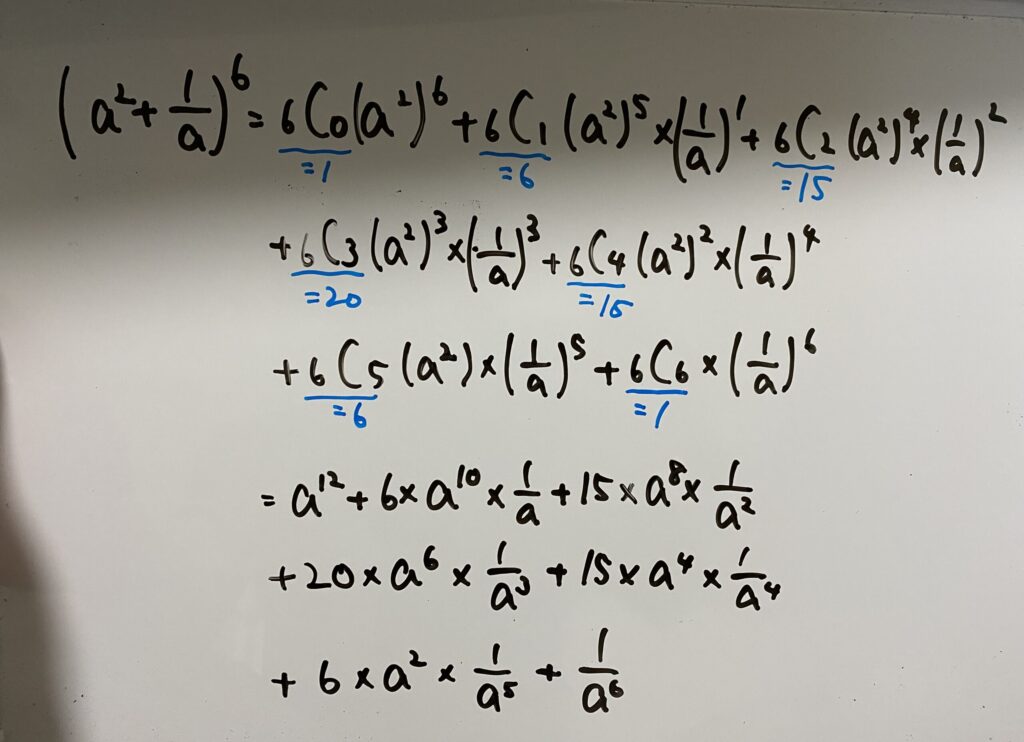
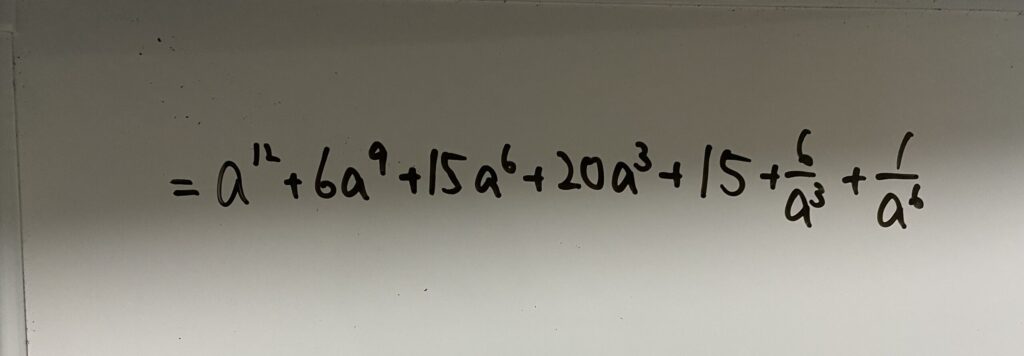
答え…
練習問題②
次の式の展開における[ ]内に指定された項の係数を求めなさい。
(1)
(2)

練習問題①に次いで頻出する問題ですね。一般項の求め方を知っていれば全然難しくありません。
練習問題①より指数が大きくて、二項定理を書き出して見つけるのは骨が折れますよね?なので一般項の求め方を使います。
です。
この式の各文字に代入して、適切なrを探せば求められます。
(1)二項定理
したがってr=3を代入して
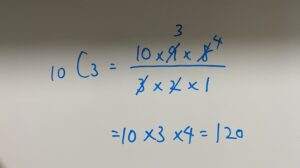
答え…15000
(2)二項定理
したがってr=3を代入して
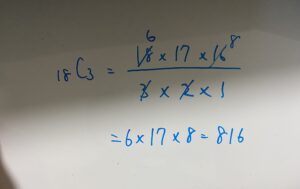
答え…102
これまで項が2つの場合を学んできました。ひとつ増やしてみましょう。


良い質問です!実は三項定理ではなくて『多項定理』になります。
項が3つ以上の場合はすべて多項定理です。
結論から

なぜこうなるのか知りたい方のために証明をしました。少し複雑なので数学が苦手な方は飛ばしてもらって結構です(^∇^)ただ一般項の式は覚えてね!
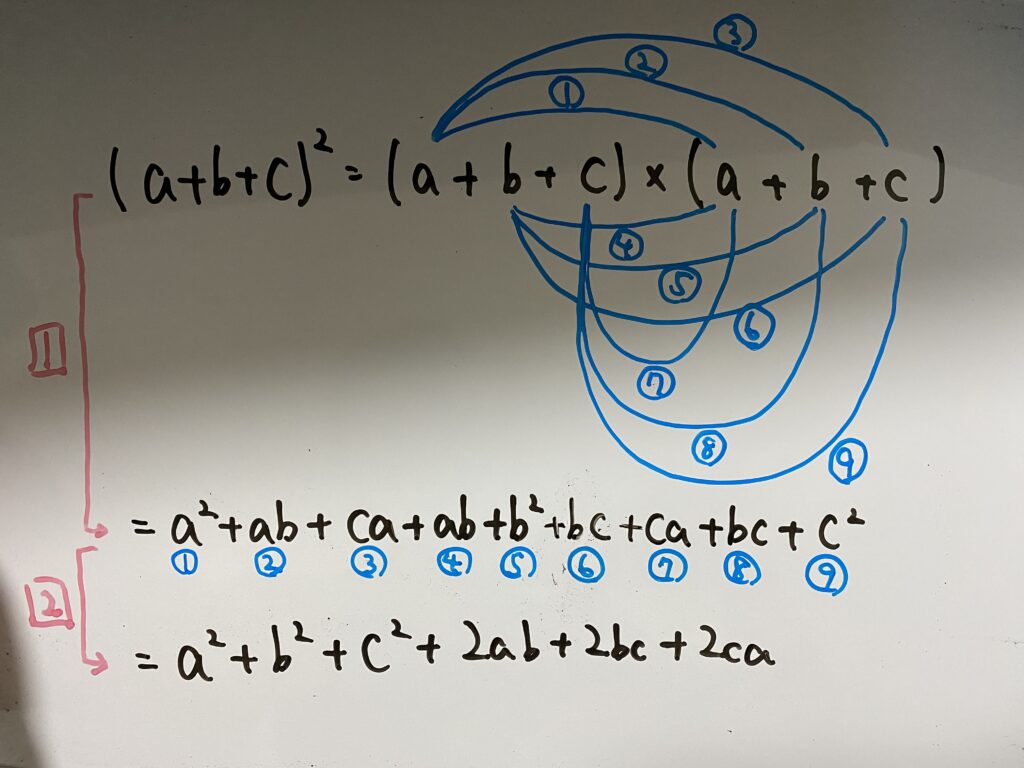
この時1、2で
1…全ての組み合わせを書き記す
2…同じ組み合わせを足している
ここで理解して欲しいのは
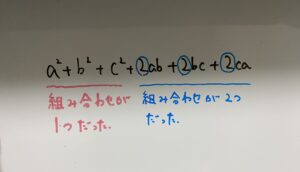
組み合わせの観点から図示すると
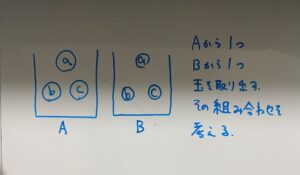
こんなイメージ。
その組み合わせの個数が係数になります。
この前提を理解しておいてください。
n次式
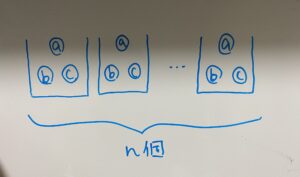
こんなイメージ。
今回求めるのは
『n個の入れ物の中からaをp個、bをq個、cをr個取り出す組み合わせの個数』
を求めれば良いということになります。
考え方としては
❶:n個の入れ物のうちp個から玉aを取り出す
❷:❶で取り出した入れ物以外のうちq個から玉bを取り出す
❸:❶❷で取り出した入れ物以外からすべて(r個)玉cを取り出す
それぞれの組み合わせを求めればオッケー。
❶:n個からp個取り出すので
❷:❶で取り出した入れ物を除くと残りの入れ物はn-p個。そこからq個玉bを取り出すので
❸:❶❷で取り出した入れ物を除くと残りの入れ物はn-p-q個。そこからr個玉cを取り出すので
❶〜❸の組み合わせが分かりました。あとはそれぞれ掛けるだけです。
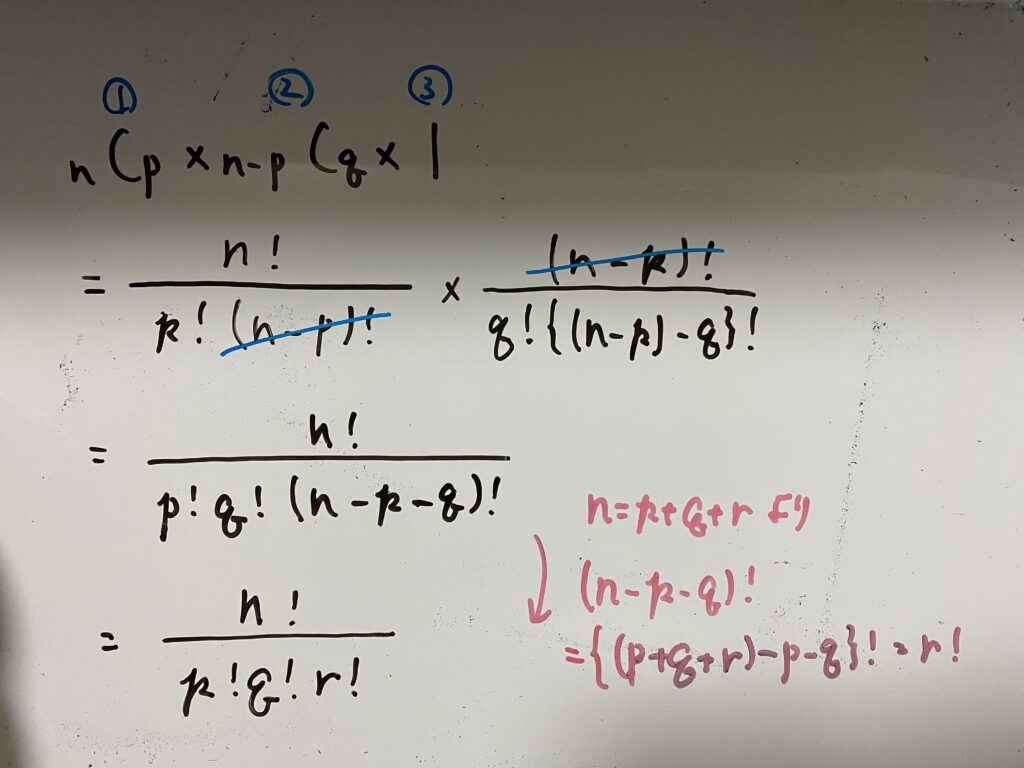
以上が解説です。

解説の前にも言った通り、少し難しいので公式を覚えておくだけで結構です。
練習問題③
の展開式における

公式に当てはめるだけの簡単なお仕事です。
答え…-864
まとめ

頑張ってたくさん解きましょうね(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
楽しい数学Lifeを!



