
ジル
みなさんおはこんばんにちは。
クリぼっち確定のジルでございます!
今回からしばらく『図形と数量』の領域を解説しようかと思います。
まずは基礎の部分を丁寧に解説していきます。
定義(絶対覚えること!)
次の三角形を例にします。
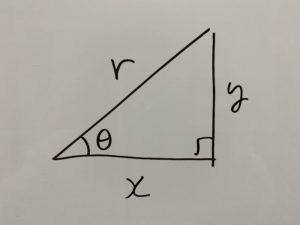
この時次の3つを定義します。
これは必ず覚えましょう。
一応簡単な覚え方がありまして、少しこじつけなのですが
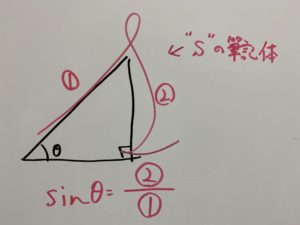
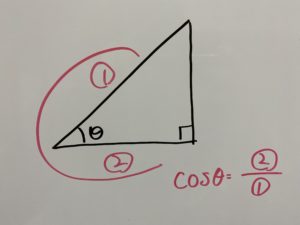
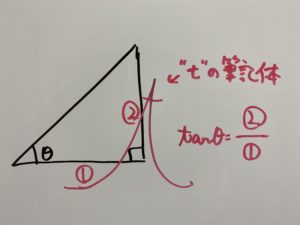
という感じで私は覚えました。

ジル
割と頭に残りましたよ!
ここで少し確認しておきます。
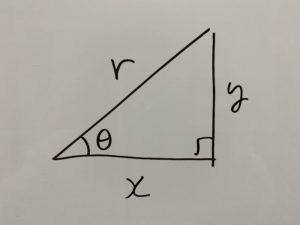
この時は
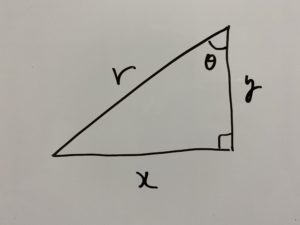
この時は
ではないですからね!
これは”
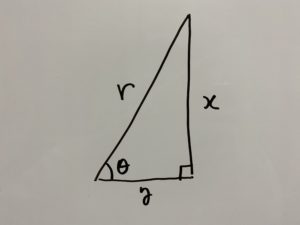
このように三角形を回転させると使えます。なので
となります。
そしてもう一つ
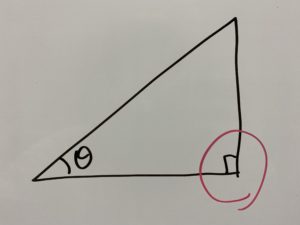
ここが90°じゃなければいけませんからね!
![]()
練習問題
さて
各ケースでの

ジル
下にまとめて答えを書いておきますのでね!
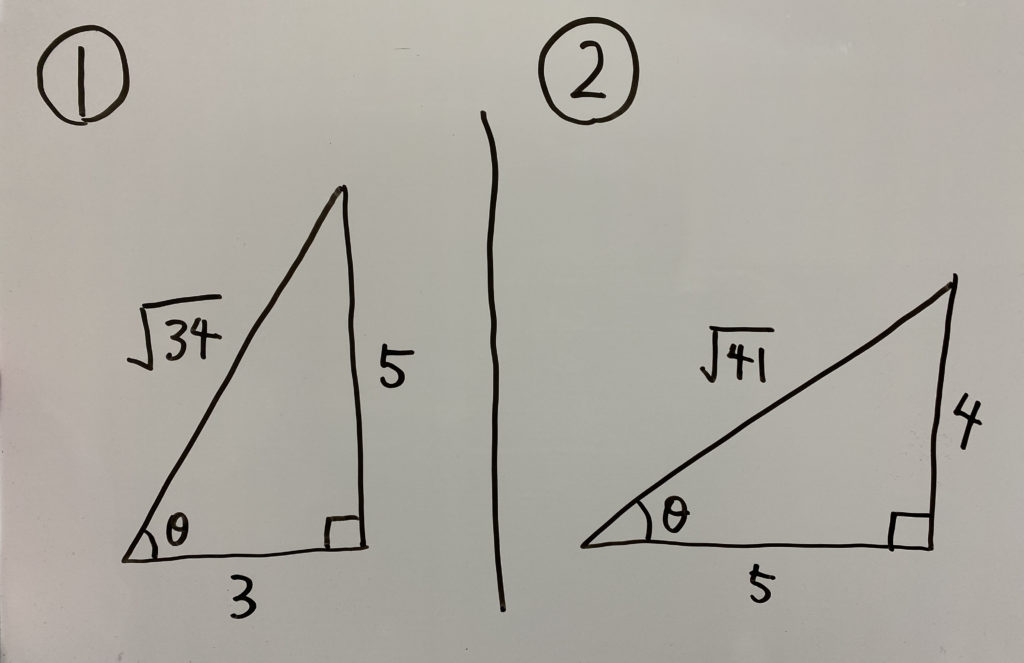
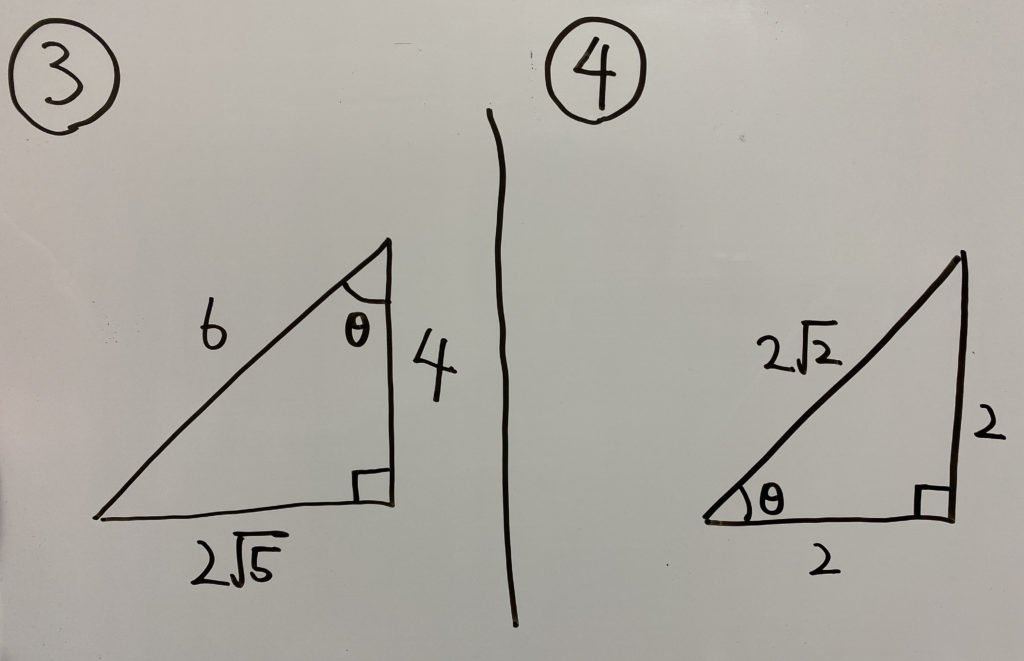
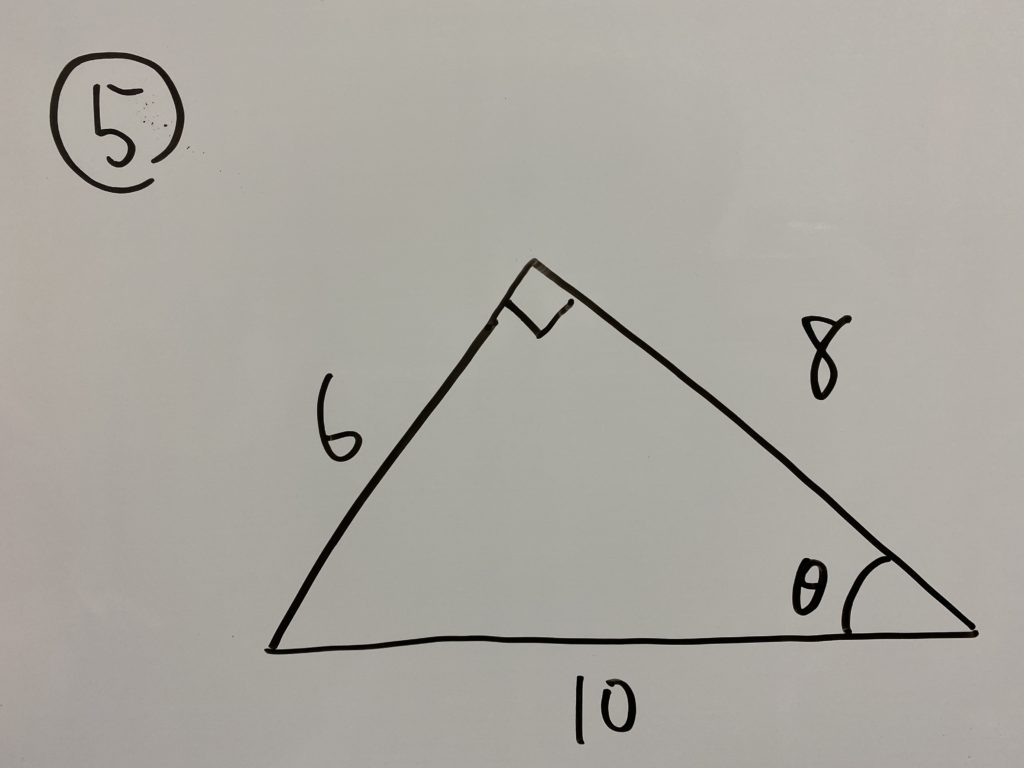
解答
①
②
③
④
⑤

ジル
どうでしたか?
少し引っ掛けっぽい問題も入れました。
最後に
次は三角比に関する他の公式を解説しようと思います。

ジル
楽しい数学Lifeを!



