みなさんおはこんばんにちは。
新しい加湿器を買おうか検討しているジルでございます！
前回に引き続き二次不等式の応用問題を解説します。
今回は少し難しめの問題になっております。
頑張ってついてきてくださいね！
$y=x^2+2kx+2k^2-k+1(kは正の定数)$について
頂点を$k$を用いて表しなさい。
まずは平方完成しましょう。もし忘れた方は下の記事を一度ご覧ください。
$y=\{(x^2+2kx+k^2)-k^2\}+2k^2-k+1=(x+k)^2+k^2-k+1$
したがって頂点は$(-k,k^2-k+1)$
$-1 \leqq x \leqq 1$の時、最小値が$２k$となる時の$k$の値を全て求めなさい
こちらを解きます。
パッと見けっこう難しそうですよね？こういう時まずはわかる限りの情報を集めるところから始めます。
テンプレな解き方はありません。泥臭くてもいいのでできる限り情報を集めて、その中で使えそうなものを見つけましょう。
・頂点の範囲を考えてみます。
$x$座標について
$-k$は、$k$が正であるため$-k \lt 0$
$y$座標について
$k^2-k+1=(k-\frac{1}{2})^2+\frac{3}{4}$
$(k-\frac{1}{2})^2 \geqq 0$のため、
$k^2-k+1=(k-\frac{1}{2})^2+\frac{3}{4} \gt 0$
ということで今回の二次関数の頂点は(負,正)なんです。
したがって今回考えるグラフのパターンは
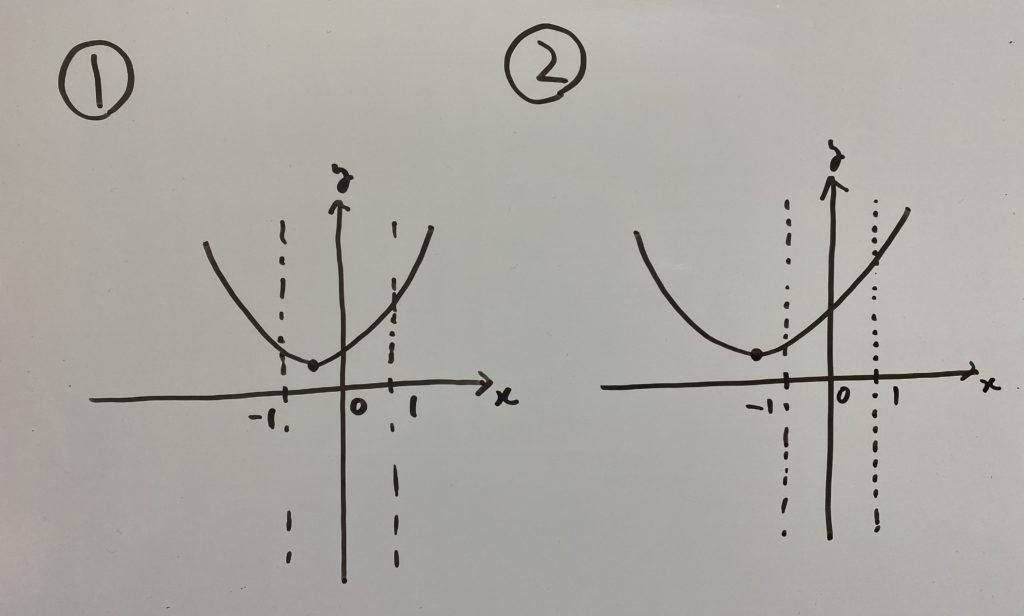
となります。
各場合を考えましょう。
①$-1 \leqq -k \lt 0$即ち、$0 \lt k \leqq 1$の時
最小値は次の点です。
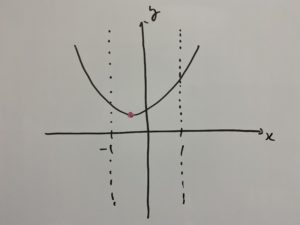
なので
$k^2-k+1=2k$が成立します。これを解くと
$k^2-3k+1=0$
解の公式を使いましょう！
$k=\frac{-(-3)\pm\sqrt{(-3)^2-4 \times 1 \times 1}}{2 \times 1}=\frac{3\pm\sqrt{5}}{2}$
ここですぐに答えとしてはいけません。条件を満たしているか確認する必要があります。
最初に$0 \lt k \leqq 1$であると言いましたね？
$$\frac{3\pm\sqrt{5}}{2}$$
がこの条件を満たしているか確認する必要があります。
注目すべきは$2^2 \lt (\sqrt{5})^2 \lt 3^2$ですね？なので$2 \lt \sqrt{5} \lt 3$であります。
それを踏まえて見てみましょう！
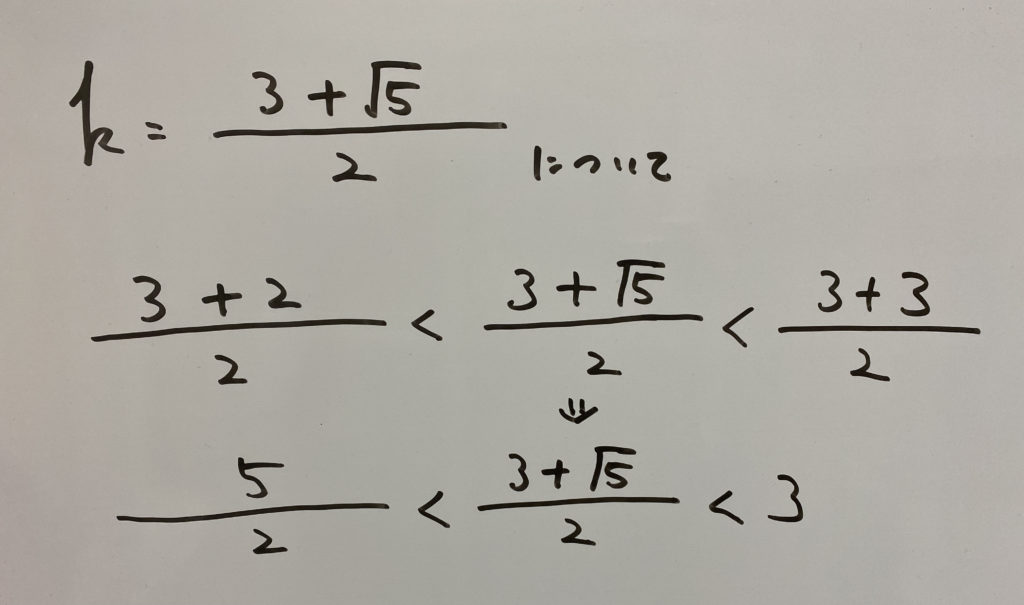
したがって答えに適しておりません。
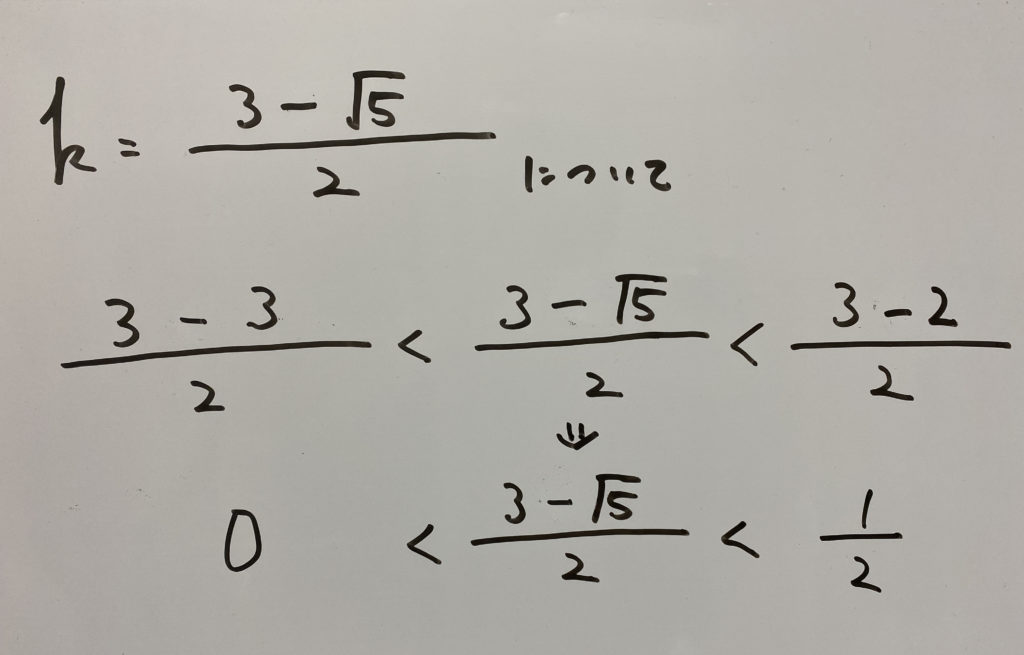
したがって適しております。
②$-k \lt -1$即ち、$k \gt 1$の時
最小値は次の点です。
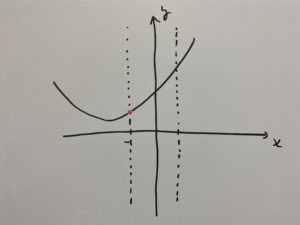
つまり$x=-1$の時最小値$2k$をとります。
なので$y=x^2+2kx+2k^2-k+1$に$x=-1$、$y=2k$を代入できます。
$2k=(-1)^2-2k+2k^2-k+1$
$2k^2-5k+2=0$
$(2k-1)(k-2)=0$
$k=\frac{1}{2},2$
$k \gt 1$を満たすのは$k=2$
以上のことから答えは、$\frac{３-\sqrt{5}}{2}$、$2$
最後に
今回はなかなかに難しい問題をやりました。
次回からはしばらく『図形と計量』の分野を記事にしようかと思っています。
楽しい数学Lifeを！
