
みなさんおはこんばんにちは、ジルでございます!
今回は高校数I二次関数「最小値・最大値」の応用問題を解説します。
なんと
ではやっていきましょう。
ちなみに今回は1問だけです。
今記事ではこの1問を徹底的に解説したいと思います。苦手な方から得意な方まで皆満足できるようにします。

別でただただ問題を解く記事を書こうかと少し考えております( ^ω^ )
早速解いていく!
今回紹介する問題を解くには前回の基礎問題の記事で書いた知識が必要です。
二次関数の基礎に不安のある方はご一読ください。

こちらを解いてみましょう。
ポイントは場合わけです。
前回、頂点が定義域に入っているか入っていないかで最小値・最大値が変わってくるとお話ししました。
ということでまずは頂点を求めるところから始めましょう!
つまり頂点は
場合わけをしていく。(何通りすればいいか)
では場合わけします。
とりあえず分かるのは『頂点が定義域に入っている場合』と『頂点が定義域に入っていない場合』の2通りです。
よし、じゃあこの2通りを検証すれば大丈夫!…ではないんですねこれが。
例えば
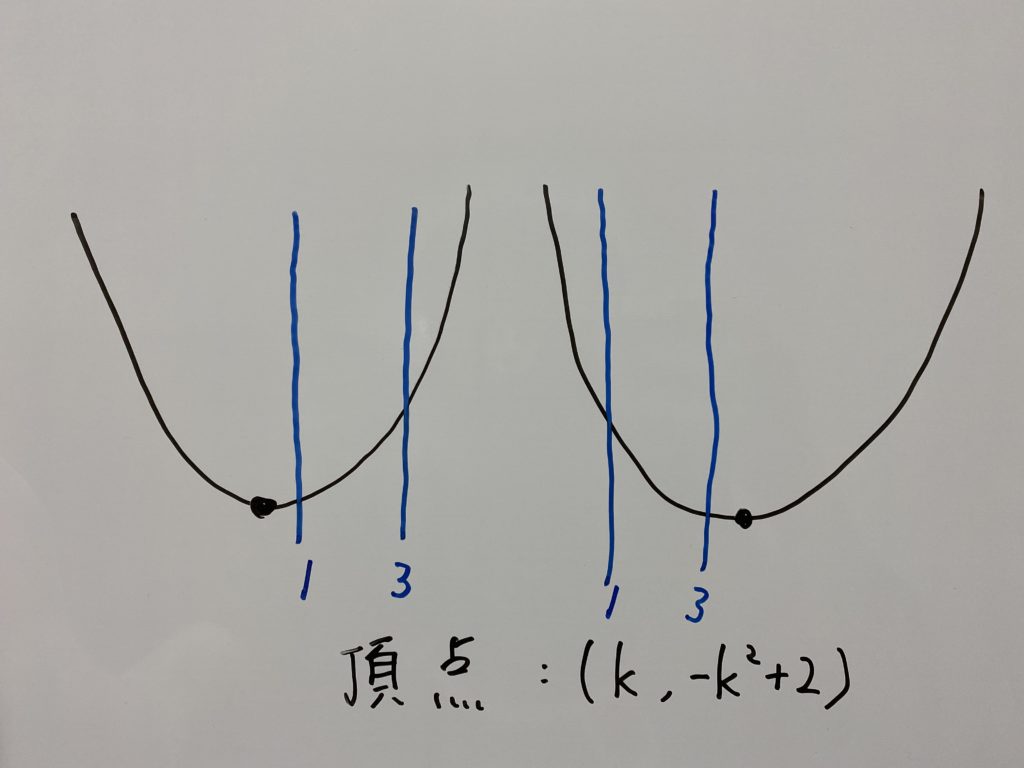
この2つのグラフについて、両方とも頂点は定義域の外ですが、それぞれ最小値・最大値の
そして実は定義域の中でも場合わけをしなければなりません。というのも
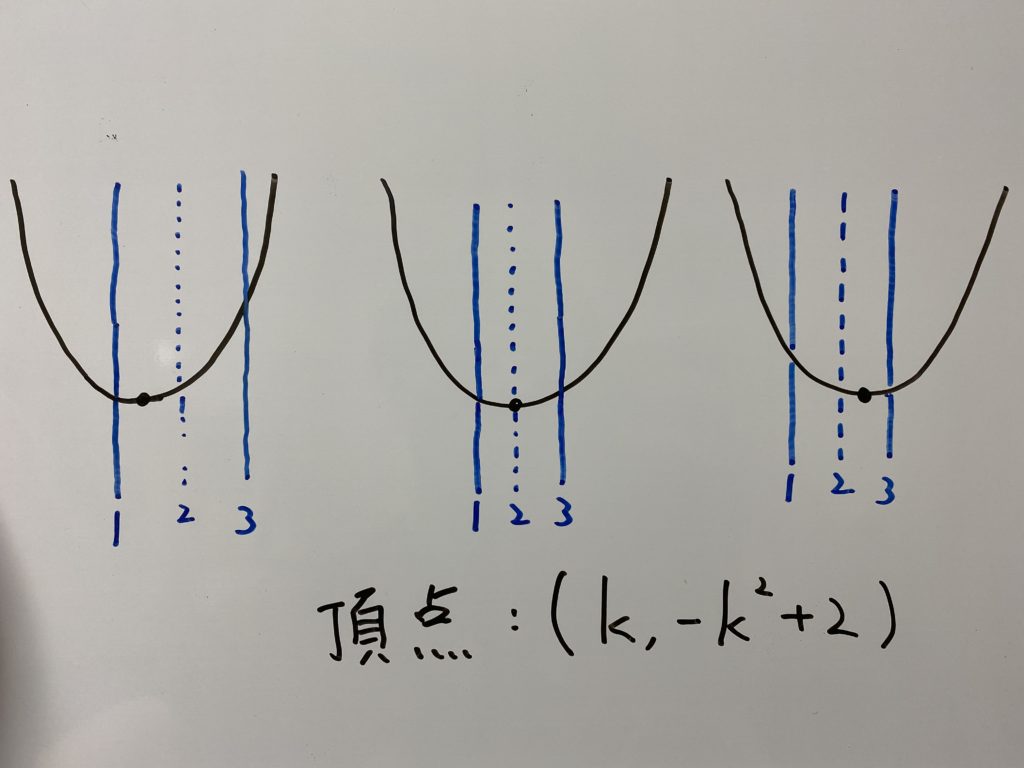
この3通りでも最小値・最大値、そしてその際の
よってここも場合わけする必要があります。
以上のことから
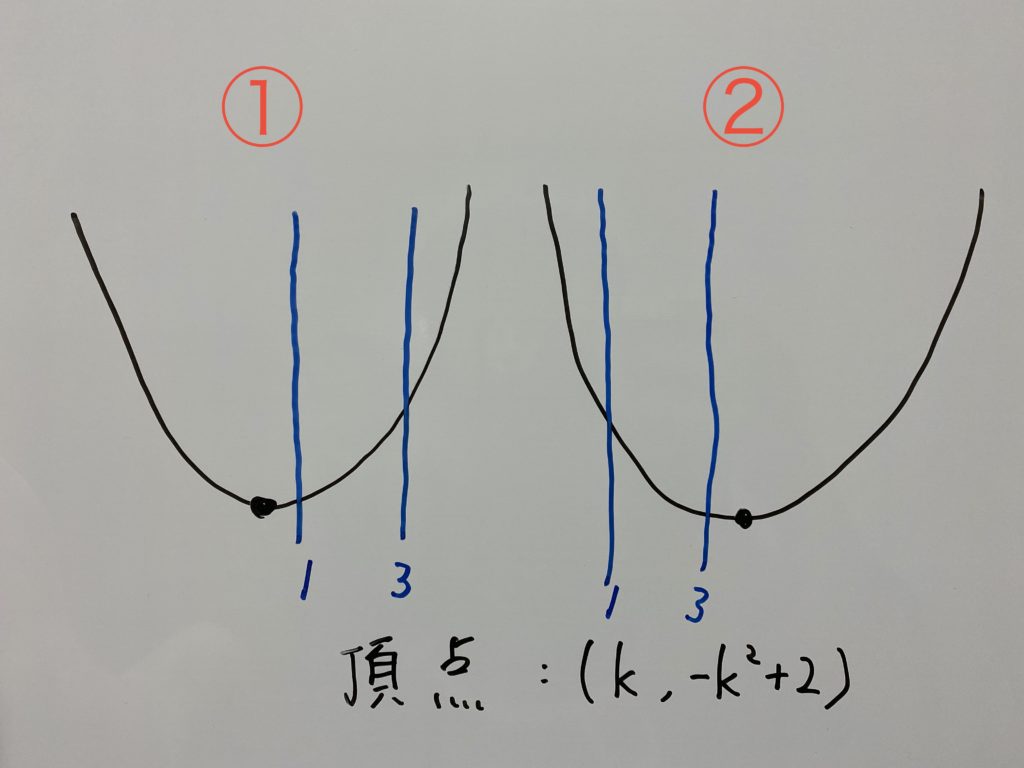
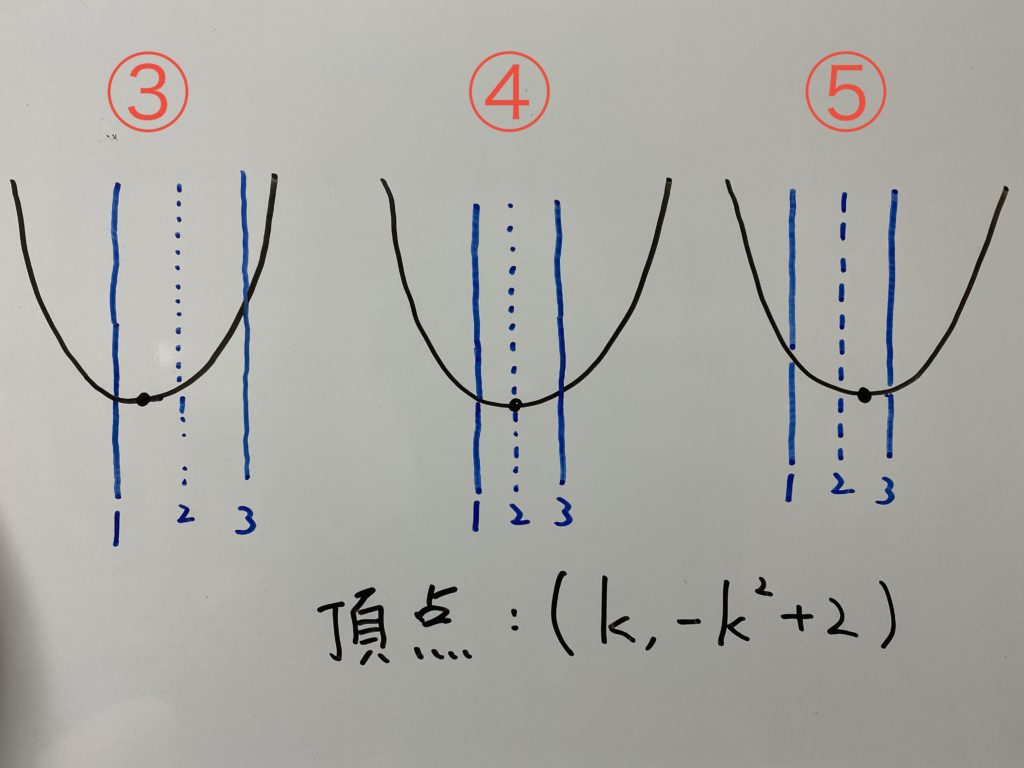
この5通りで場合わけをすれば解けます。

めっちゃ多いやん!難しそう…_:(´ཀ`」 ∠):

大丈夫!場合わけさえしっかりできればそのあとはパパッとできます。
では以前の記事にて確認したことを復習しながら解説します。
頂点が定義域に入っていない場合(①、②)
この場合は
最小値は「定義域の左端と右端のうち、頂点に近い方」
最大値は「定義域の左端と右端のうち、頂点に遠い方」
最小値は「定義域の左端と右端のうち、頂点に遠い方」
最大値は「定義域の左端と右端のうち、頂点に近い方」
でしたね?覚えていますか?絶対覚えてね!
今回
①から順番にやってみましょう。
①の場合
この場合は
②の場合
この場合は
頂点が定義域に入っている場合(③、④、⑤)
今回は
頂点の
定義域の左端と右端、それぞれと頂点の
でしたね?覚えてね!
ではではやっていこう。

あと少しです。がんばれ(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
③の場合
この場合最小値は頂点、最大値は
④の場合
これは少し特殊な例です。
最小値は頂点なのですが、最大値は

これは二次関数が左右対象であるため起こるんですね!
kの値が具体的に決まっているので、kに2を代入してしまいましょう。
最小値は頂点なので、
最大値は
今回は
今回は
⑤の場合
この場合は
この時は、頂点で最小値、
したがって答えが出ましたね!
答え:
最後に
かなり壮大な問題になってしまいました。

問題考えている時はこんなに超大作になるとは思いませんでした笑。
これが理解できて、解けるようになれば理解度は上がっていると思っていいでしょう!
次は他の応用問題をやろうか、次の単元である二次方程式を解説するか迷っております。
いずれにせよ、苦手な方でも分かりやすいように心がけていきますのでよろしくお願いします(*´∀`*)

楽しい数学Lifeを!
![]()



