
みなさんおはこんばんにちは、ジルでございます!
今回は二次関数の最大値・最小値を勉強しましょう。
この分野を勉強するには、二次関数の基礎部分、軸・頂点の求め方を知っておく必要があります。
関連する記事を下に貼っておいたので、不安な方はぜひご覧ください!


定義域について(おまけに値域も)
まずは「定義域」「値域」の復習をしましょう。
定義域…
値域…
になります。
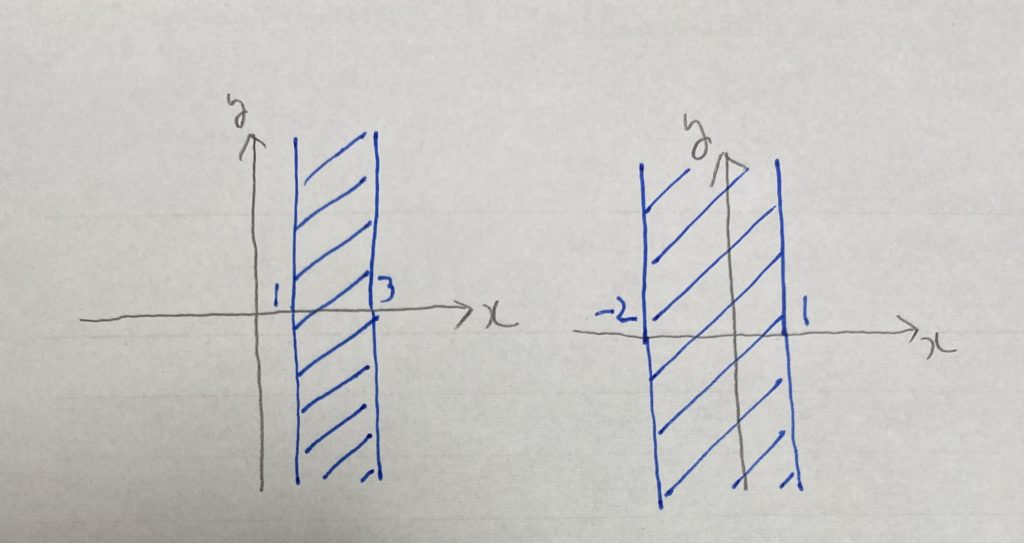
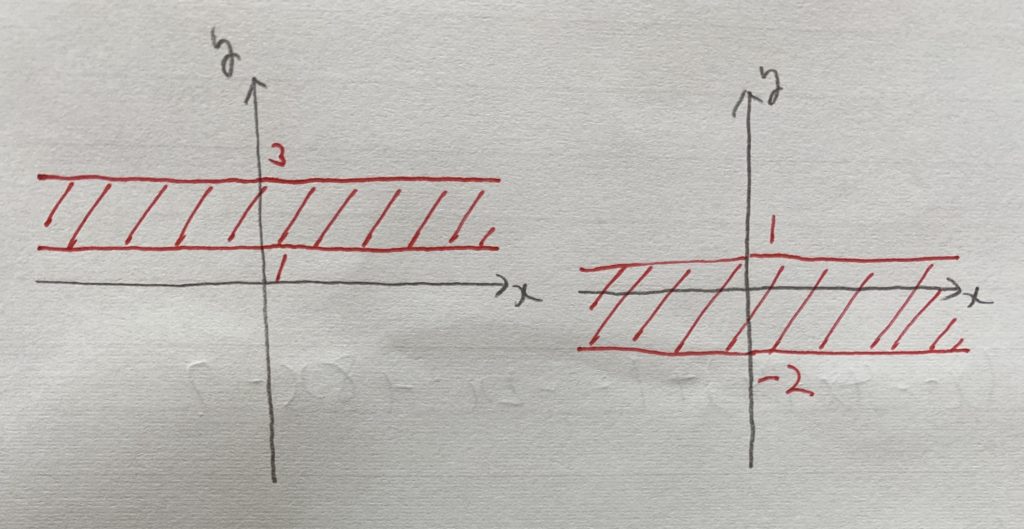
最大値・最小値の求め方
では本題に入りましょう。
最大値・最小値を求めるということは、
ということです。
二次関数で、最大値・最小値を求める問題では先ほど復習した「定義域」が指定されているパターンとさせていないパターンがあります。
それぞれの場合で勉強しましょう。
定義域がない場合
定義域がない場合は、二次関数の性質上、最大値または最小値が存在しなくなります。
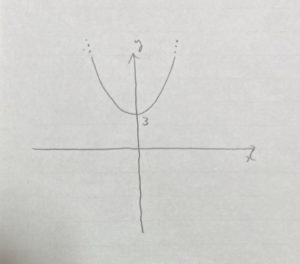
グラフを実際に書いてみると分かります。
最小値、即ち一番小さい
ところが最大値はないのが分かりますか?何故ならこの二次関数は永遠に上に続いているからです。
答え 最小値:3 最大値:なし
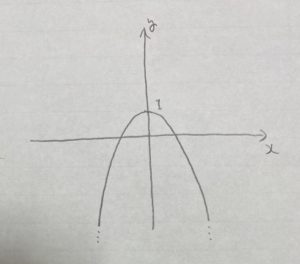
最大値は頂点の
一方最小値はありません。グラフを見てわかる通り、下は永遠に続いていますから。
答え 最小値:なし 最大値:1

一旦まとめてみましょう。
定義域がある場合
次に定義域があるパターンを勉強しましょう!
この場合は最大値・最小値ともに存在します。
求める方法ですが、慣れないうちはしっかりグラフを書いてみるのがいいです。
慣れてきたら書かなくても頭の中で描いて求めることができるでしょう。
まずは簡単な二次関数から始めます。
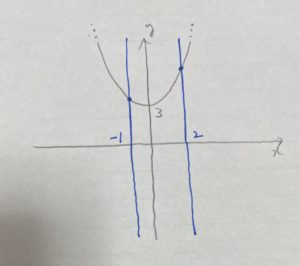
実際に書いてみると分かりやすいです。
最小値(一番小さい
最大値(一番大きい
答え 最小値:3 最大値:7
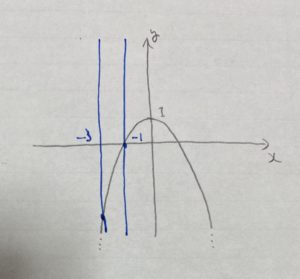
最小値はグラフから、
最大値はグラフから、
答え 最小値:−8 最大値:0
最後に 次回予告も
今記事で、二次関数の最大値・最小値の掴みは理解できましたか?
しかし実際にみなさんが定期テストや受験で解く問題はもっと難しいと思われます。
次回はこの最大値・最小値について応用編のお話をします!

テストで出てもおかしくないレベルの問題を取り上げるつもりです。
数学が苦手な方でも理解できるように丁寧を心掛けますのでぜひ読みにきてください!

楽しい数学Lifeを!



