
みなさんおはこんばんにちは。
ダイパやりたいけどSwitchなくてできないジルでございます!
みなさん『円周角の定理』は覚えていますでしょうか?
「そんなもん聞いたことないぞ?」
そんなあなた!中学でやっているはずです。
円周角の定理
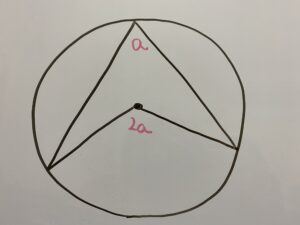
1つの弧に対する円周角の大きさは一定であり、その弧に関する中心角の大きさの半分である。

この定理好きなんですよねー。なんか綺麗で!
ちなみに中心角が90°以上の場合(鈍角)も成立します。
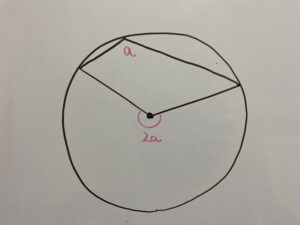
円周角の定理の逆
先程の円周角の定理のなかの「1つの弧に対する円周角の大きさは一定」に注目します。
この時
が成立する時A,B,C,Dは1つの円周上にある。

なぜこれが円周角の定理の逆になるんや?

イマイチ納得できない、分からない方は次をご覧ください。
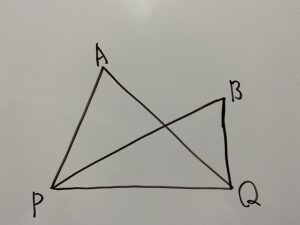
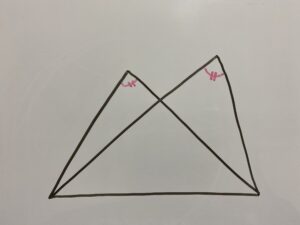
次の図を見てください。
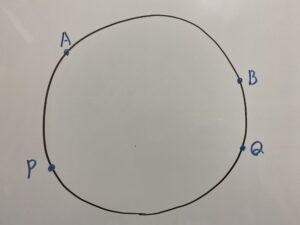
⇩
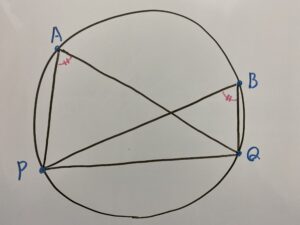
「A,B,P,Qが1つの円上にある」⇨「弧PQに対する円周角
これが円周角の定理です。その逆は
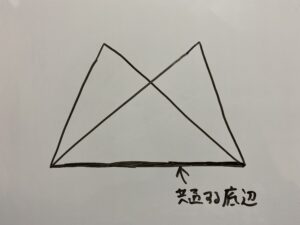
このように共通する底辺を持つ2つの三角形が存在する時、
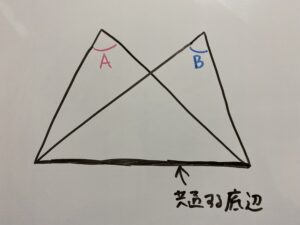
角Aと角Bが等しい時を考えます。
共通の底辺を弦としてみましょう。
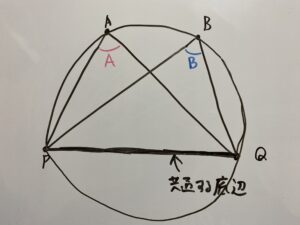
この時底辺に対する2つの角が等しい時、A,B,P,Qは1つの円上にあることになるのです。
練習問題
では円周角の定理の復習も兼ねて練習問題を解いてみましょう。
問1
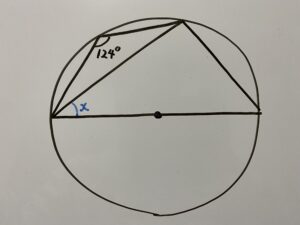
この時xは何度か答えなさい。
はいこちらは円周角の定理を使う問題です。もういかにも使いそうなオーラが漂っていますね!
円周角を使う問題で大事なことは線を引くことです。

基本的にそのままでは答えに辿り着けないことが多いです。必要な線を引くことで答えが見えてきます。

どこに線を引くかは決まっていますか?

決まっておりません。もうこれは経験ですね( ^ω^ )
たくさん問題を解けば分かってきますよ!
ちなみに正しい線は1本とは限りません。
ではそろそろ解いてみましょうね!
解説
さてまずは正しい線を引くことから始めましょう!
先にネタバレしておくと、2通りの正しい線があります(^∇^)

もし他にも別解があればぜひ教えていただきたいです!
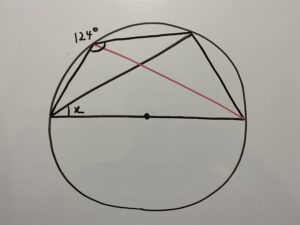
解1

この問題を一目みてパッと閃いたのがこちらの線です。
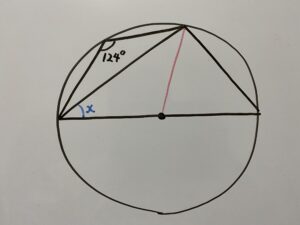
この線です!ある程度問題をこなしている人ならとりあえずここに引くはずです。

線を引いてみて上手くいかなかったら別のところに線を引いてみればいいんです。
パッと思いついた線を使ってやってみるのが大事!
では解いてみます。
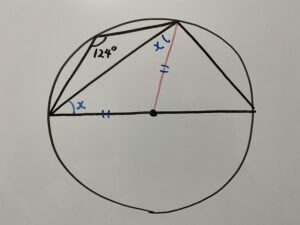
この時ここの角度、分かりますか?すでにみなさんは習っているはずです。
この分野ではメチャクチャ使いますのでもし忘れていたらここでしっかり覚えましょう!

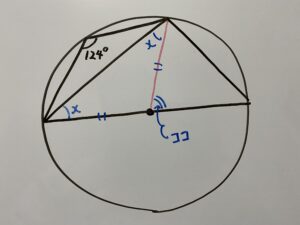
はい、もうこっちのもん
円周角の定理より次の等式が成立します。
解2
実はここに線を引いても答えを導けます。

この線は記事を書いていく中でふと閃いた線です!
まず「円周角の定理」より
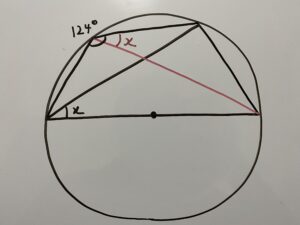
であることが分かります。

1つの弧に対する円周角の大きさは一定であり、その弧に関する中心角の大きさの半分である。
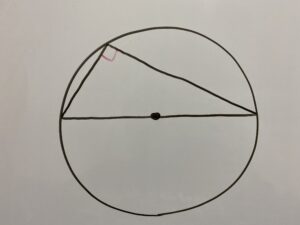
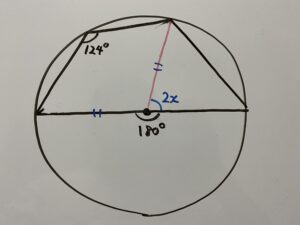
またもうひとつ、円周角の定理の応用で、弧が半円の時は

このように円周角は必ず90°になります。つまり
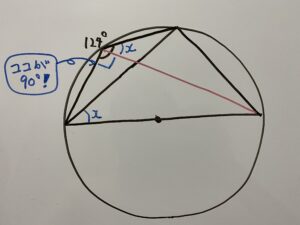
したがって
答えは34°
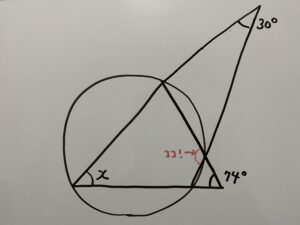
問2
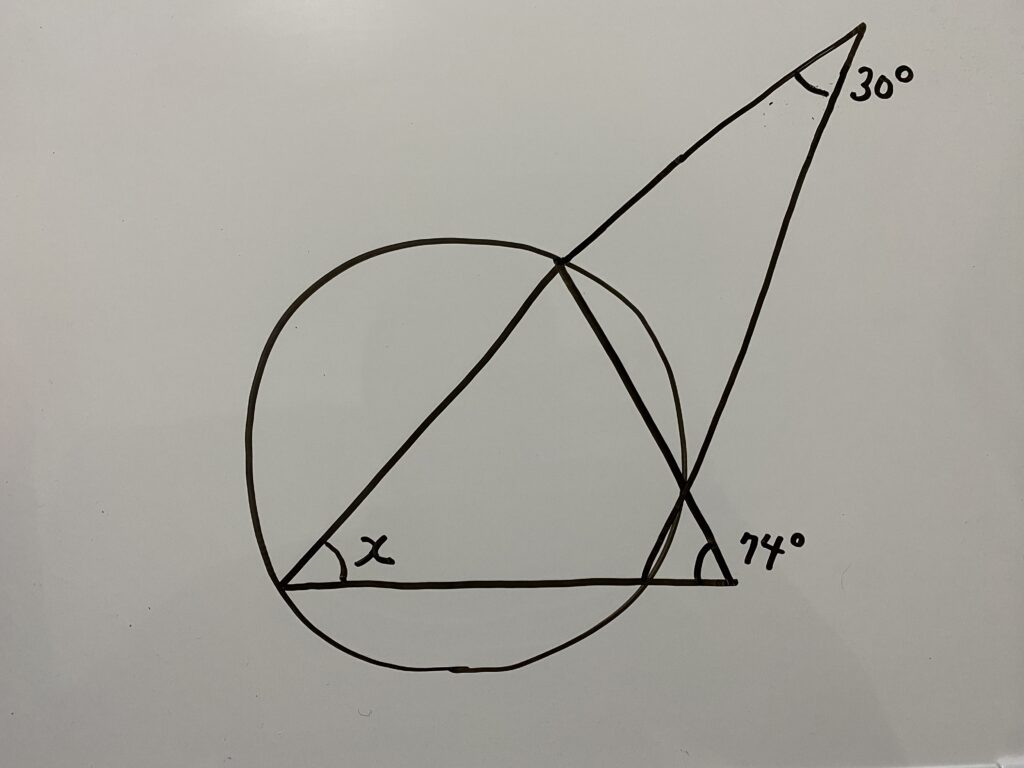
この時xは何度か答えなさい。
実はこちらも2通りの解法がございます。
です。

主流なのは解1でしょうね。ただ解2のように定理を知らなくても答えを導き出せることを覚えておいてね!
勉強を進めるために必要な定理と、覚えなくても何とかなる定理がありますのでその辺り効率的に勉強しましょうね(^∇^)
解1(円に内接する四角形に関する定理を使う)
この解で使用する定理を紹介します。
このように四角形が円に内接している時、次の2つが成立する
①四角形の対角の和は180°
②四角形の内角は、その対角の外角に等しい
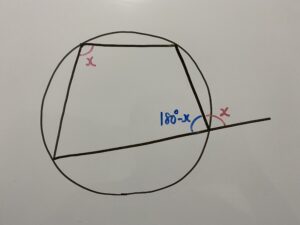

①と②は同じことを言っているだけなので片一方だけ覚えとけばええで!
では解いていきます。

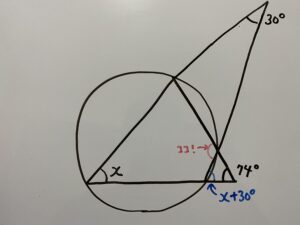
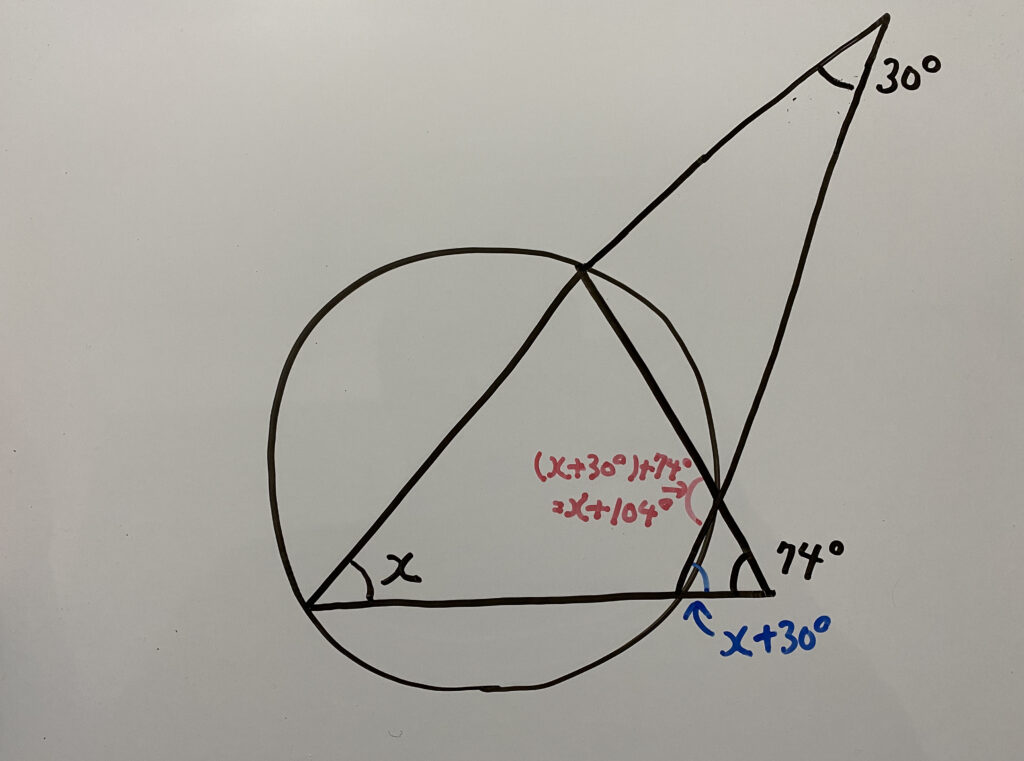

もろたで○藤!
ということは「円に内接する四角形の定理の①」を使えば
解2
こちらは「円に内接する四角形の定理」を使わない解法です。
この解法を使うには線を引く必要があります。

何度も言いますが、こういう線を見つけられるかどうかは『経験値』がものをいうのでたくさん問題を解きましょうね!
今回使う線は次の青線です。なお2本。
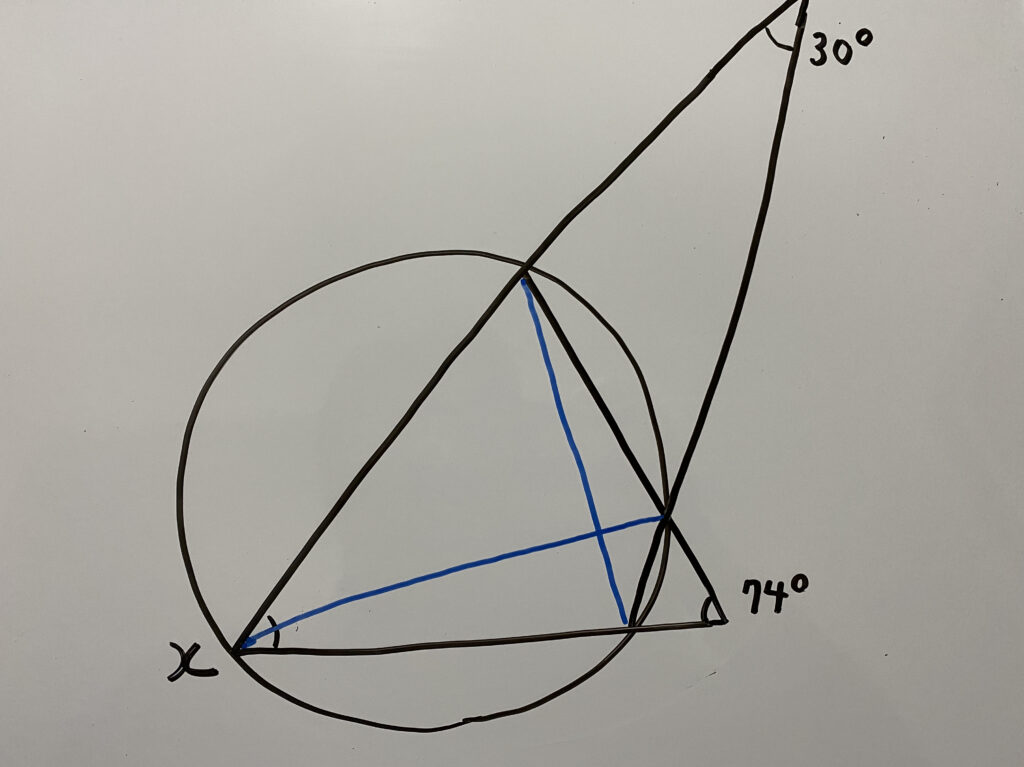
円周角の定理を使うと
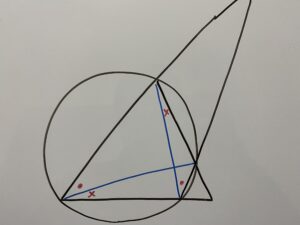
であることが分かりますね?
つまり
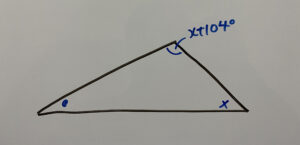
ここで解1でも使ったこちらの定理から分かる角度を利用します。

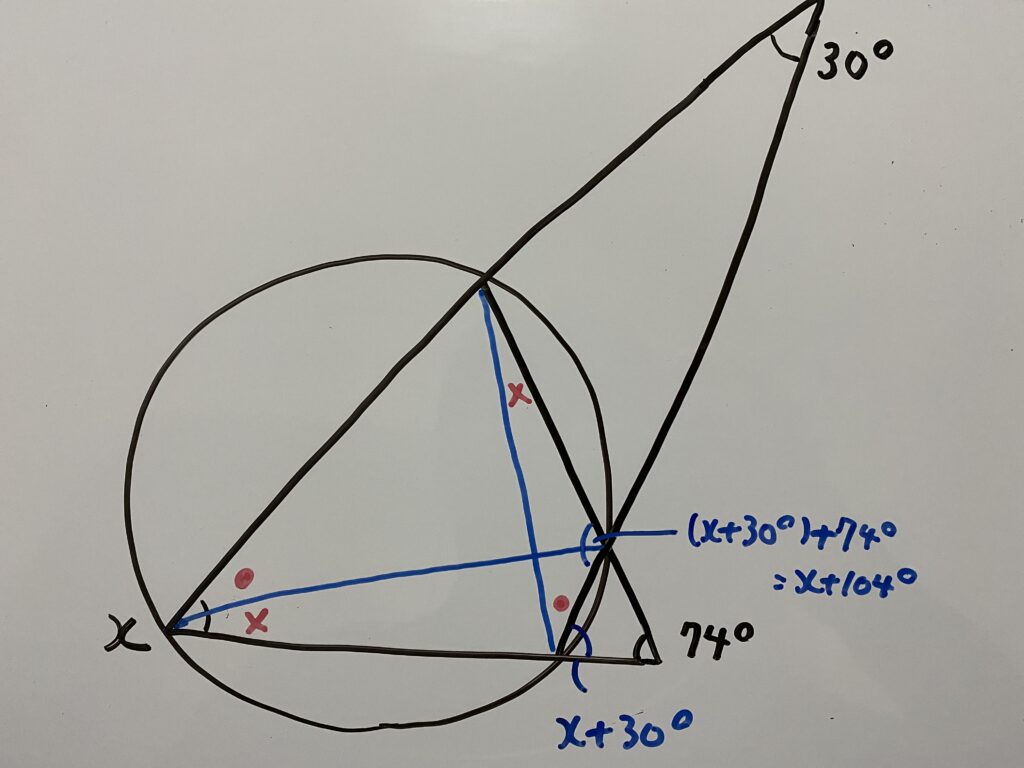

もろたで○藤!!!
まとめ

1つの弧に対する円周角の大きさは一定であり、その弧に関する中心角の大きさの半分である。
この時
が成立する時A,B,C,Dは1つの円周上にある。
このように四角形が円に内接している時、次の2つが成立する
①四角形の対角の和は180°
②四角形の内角は、その対角の外角に等しい



ポ◯モンだって経験値で強くなるでしょ?それと同じです( ^ω^ )
次も円に関する内容を解説しますのでぜひご覧くださいね!

楽しい数学Lifeを!



