
みなさんおはこんばんにちは。
秋がすっ飛んで冬が来て少し残念なジルでございます!
今回は難しそうな定理を2つ解説します。
チェバの定理
まず△ABCを用意します。
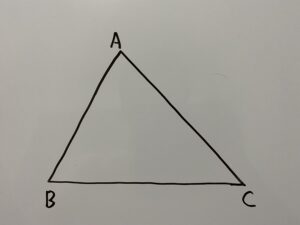
各頂点から対面する辺へ線を引きます。ここで大事なのは、その3本の線は△ABCの中の一点で交わるようにすることです。

三角形の外で交わる場合でも成立しますが今回は三角形の中の場合をやります。
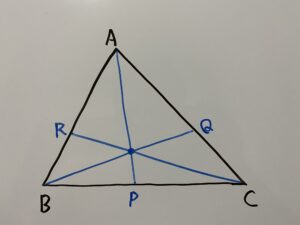
この時
が成立します。これが『チェバの定理』です。

なんだか難しそうな定理ですね:(;゙゚’ω゚’):
ちなみに
でもいいです。
少しわかりやすくするために分母と分子で色分けしましょう。
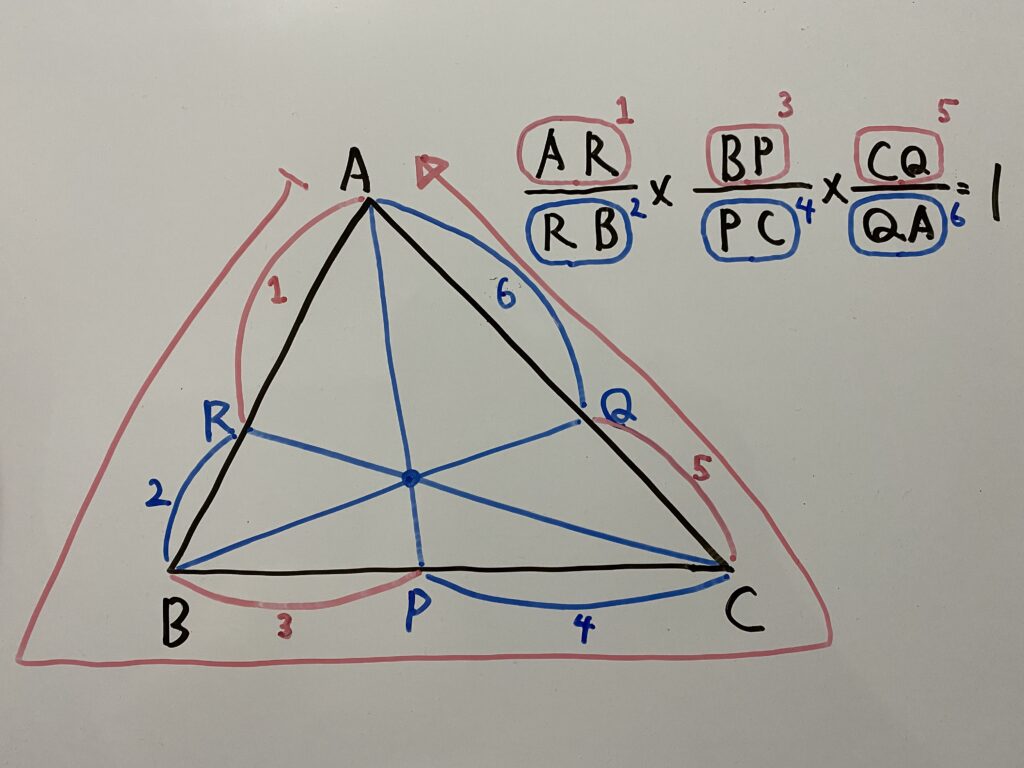
ぐるーっと回っていることがわかりますね?これで覚えましょう!
次にチェバの定理の証明をしていきましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
チェバの定理の証明
次のような三角形を用意します。
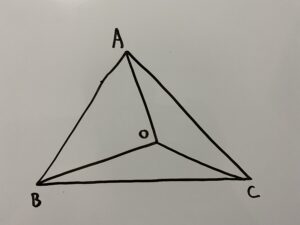
この中でOBを辺に持つ△AOB、△COBに注目します。
ここで頂点A、頂点Cから直線OBで垂線を引きましょう。
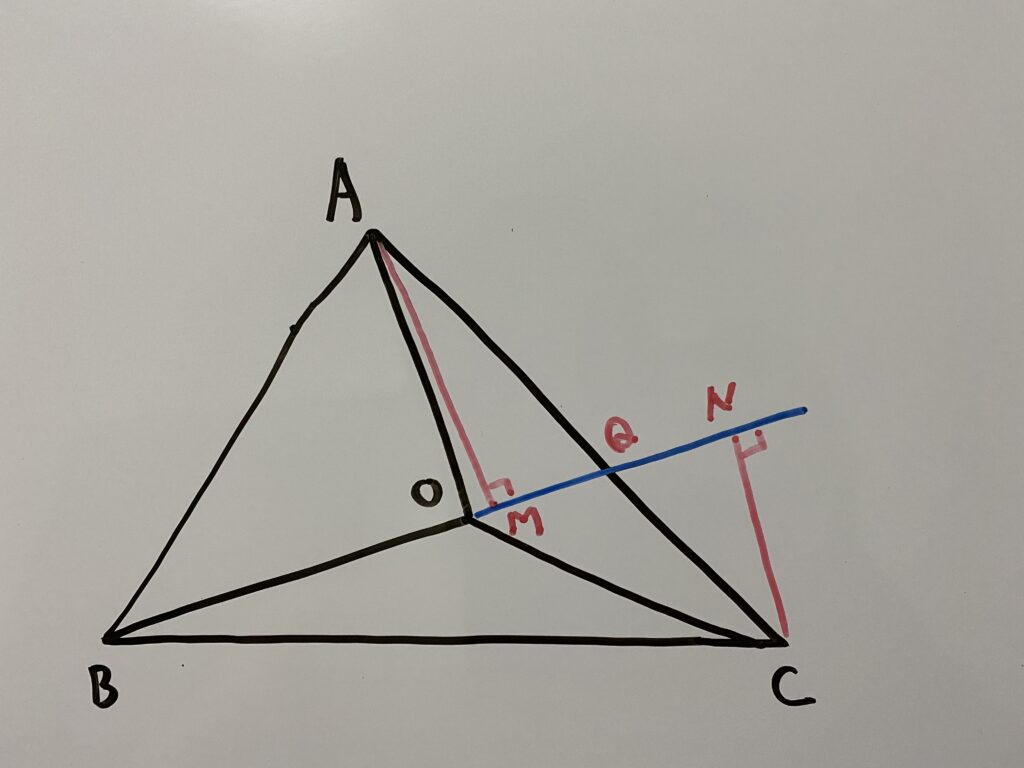
頂点Aから引いた垂線と直線OBとの交点をM
頂点Cから引いた垂線と直線OBとの交点をN
直線OBと辺ACとの交点をQ
とおきます。
ここで三角形の面積の求め方を今一度復習しましょう
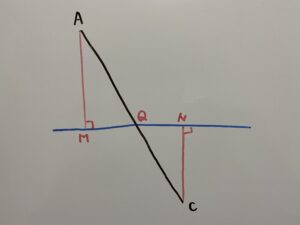
よって
また
したがって△AQMと△CQNは2組の角がそれぞれ等しいので
メネラウスの定理
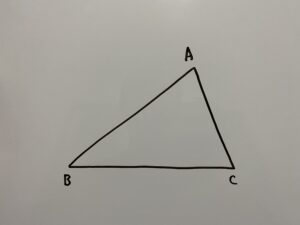
こちらもまずは△ABCを用意します。
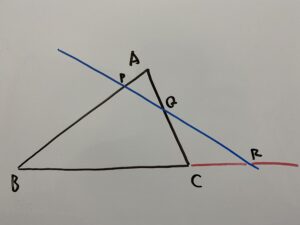
ここに1本の直線を引きます。その直線とABとの交点をP、ACとの交点をQ、その直線と直線BCとの交点をRとします。
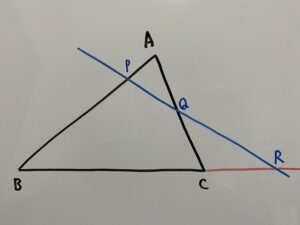
この時
が成立します。

なんかチェバの定理より覚えにくそう…(ㆀ˘・з・˘)

ぱっと見そうですね。しかし図に書き起こすと覚えやすいかもです!
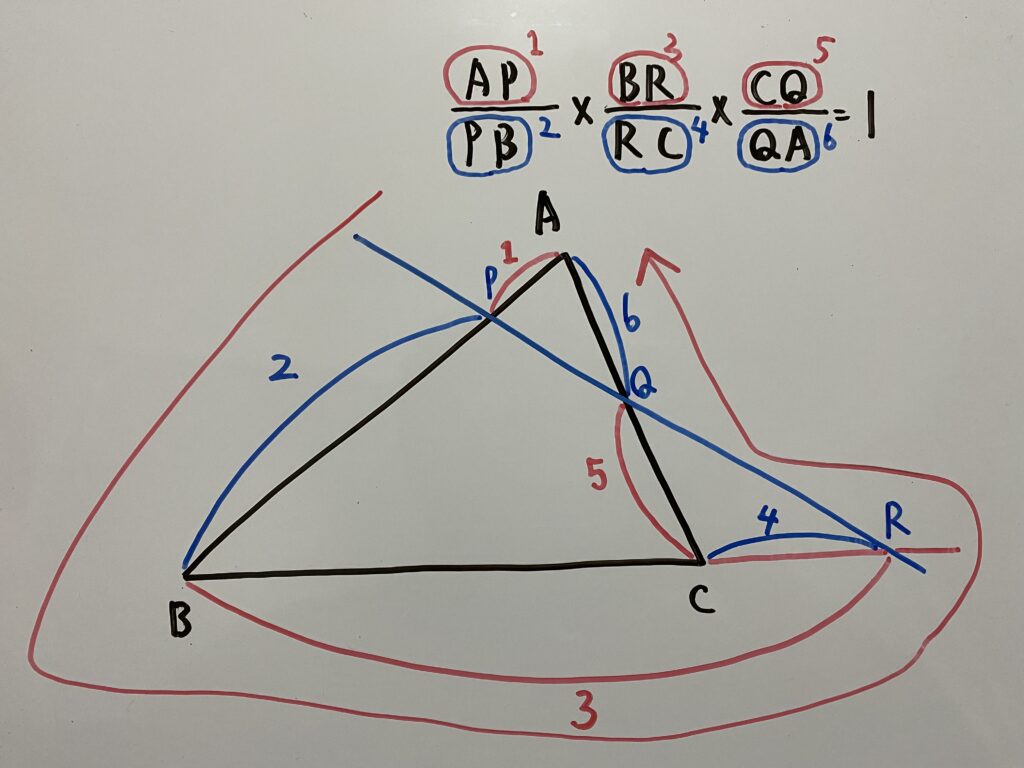
こうすると順番になっていることがわかります。
メネラウスの定理の証明
先程の図を用意します。
これにもう1本線を引きます。頂点Cを通って直線PQと平行な直線でそれとABとの交点をDとします。
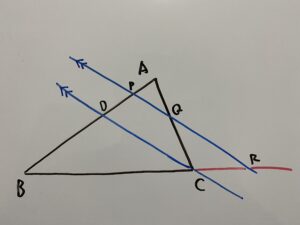
この時、△BCDと△BRPについて
△APQと△ADCについて
練習問題
ではここらでチェバの定理、メネラウスの定理を利用した練習問題を解いてみましょう。
問①
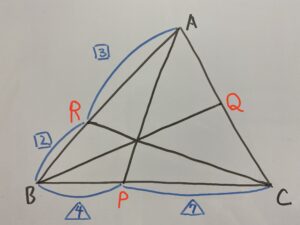
この時

同じく
よって
問②
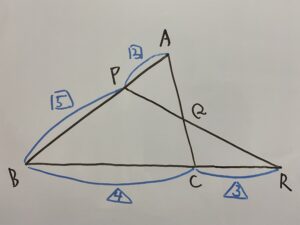
この時

$$BR:RC=7:3$よりBR=7b、RC=3b(bは正の数)で表せます。
よって
まとめ

この時

この時
今回は名前は難しそうな定理を2つ解説しました。
次は円に内接する図形の性質を解説します。

Let’s 数学Life!!



