【高校数A】『場合の数』の練習問題を元数学科が解説する！【苦手克服】

今回は『場合の数』の問題をいくつかのパターンに分けて解説しようかと思います。

この問題を解くには「樹形図」「和の法則」「積の法則」の知識が必要になります。

【高校数A】『場合の数』の基礎を元数学科が解説する！【苦手克服】

今回は【高校数学】【数A】『場合の数と確率』から場合の数について、入りの基礎を解説しました。重要な事項である「樹形図」「和の法則」「積の法則」についてまとめて、いくつか練習問題を用意しました。よかったらご覧ください。

www.zilleblog.com

2021.07.22

 

『約数の個数、及び総和』を求める問題

問

360について

（１）正の約数は全部でいくつあるか。

（２）（１）で求めた約数の総和を求めなさい。

 

まずはこちら。割とポピュラーな問題ですね。

（１）の解説

このパターンの問題は

大体はこれでいけます。

 

①素因数分解をする。

したがって$360=2^3 \times 3^2 \times 5^1$となります。

 

②積の法則を利用する。

先に結論を言ってしまいましたがこの問題は

積の法則が利用できます。

もう少し小さい数字を例にしてみましょう。

18の約数について

$18=2^1 \times 3^2$

18の約数は1,2,3,6,9,18です。

この程度の約数は暗算でも十分出せますが、どうやって導いたかと言われると

$1=2^0 \times 3^0$

$2=2^1 \times 3^0$

$3=2^0 \times 3^1$

$6=2^1 \times 3^1$

$9=2^0 \times 3^2$

$18=2^1 \times 3^2$

つまり18の約数は全て

$(2^0,2^1から1つ) \times (3^0,3^1,3^2から1つ)$

で表現できるわけです。

図にすると

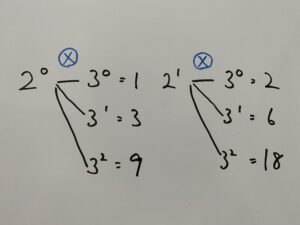
この表に覚えがありますか？そう、

 

【高校数A】『場合の数』の基礎を元数学科が解説する！【苦手克服】

今回は【高校数学】【数A】『場合の数と確率』から場合の数について、入りの基礎を解説しました。重要な事項である「樹形図」「和の法則」「積の法則」についてまとめて、いくつか練習問題を用意しました。よかったらご覧ください。

www.zilleblog.com

2021.07.22

 

この記事で説明した『積の法則』で使った表です。

このことからも積の法則が使えるのがわかりますね^ ^

したがって18の約数の個数は$(2^0,2^1から1つ) \times (3^0,3^1,3^2から1つ)$より

$2 \times 3=6$

 

では本題に戻ります。

$360=2^3 \times 3^2 \times 5^1$であることから、その約数は

$(2^0,2^1,2^2,2^3から1つ) \times (3^0,3^1,3^2から1つ) \times (5^0,5^1から1つ)$

で表現できます。

したがって積の法則から約数の個数は

$4 \times 3 \times 2=24$

答えは24個。

 

（２）の解説

総和を求めます。

正直地道に足していっても解くことは可能です。

$2^0 \times 3^0 \times 5^0 + 2^1 \times 3^0 \times 5^0 + … +2^3 \times 3^2 \times 5^1$

今回はもう少し効率的に解いてみましょう！

実は先ほどの

$2^0 \times 3^0 \times 5^0 + 2^1 \times 3^0 \times 5^0 + … +2^3 \times 3^2 \times 5^1$

は

$(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(5^0+5^1)$

を展開した式なのです！！！

$(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(5^0+5^1)$について、まずカッコの中から計算してみると

$(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(5^0+5^1)$

$=(1+2+4+8)(1+3+9)(1+5)=15 \times 13 \times 6=1170$

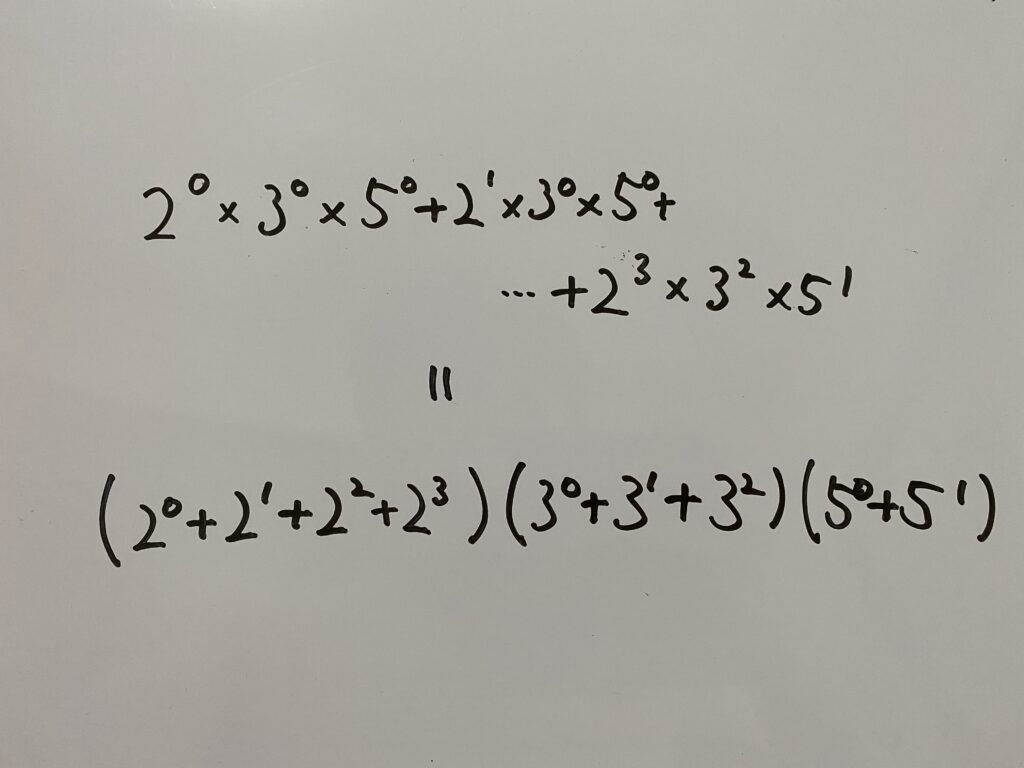
地道に計算するよりはるかに簡単に解けました！

答えは1170。

 

等式を満たす数の個数を求める問題

問

$2x+y+z=8$を満たす自然数x,y,zの組み合わせの個数を求めなさい。

 

こちらも比較的出題される形式です。

このパターンの問題を解く手順は

 

解説

 

①式変形をして１つの文字に注目する。

どの文字に注目するかと言いますと、各文字の係数を比較して一番大きい文字です。

今回はxの係数は2、yの係数は1、zの係数は1ですので一番大きいのはx。

ということでxに注目して式変形しましょう。

$2x+y+z=8$をxに注目して式変形すると

$2x=8-(y+z)$

ここで右辺について少し考えてみます。

問題に書いてあるように、x,y,zは全て自然数です。なので$x \gt 0$、$y \gt 0$、$z \gt 0$です。

よって$y+z \gt 0$であることがわかりますね？

また$8-(y+z) \lt 8$。

よって$2x=8-(y+z) \lt 8$

したがって$2x \lt 8$

xは自然数なので、$x=1,2,3$。

 

②注目した文字についての場合分けをする。

①でxの候補が1,2,3であることがわかりました。

あとはそれぞれの場合のy,zの候補を樹形図で求めればオッケーです！

（ⅰ）x=1の場合

$2x+y+z=8$に代入して

$2+y+z=8$

$y+z=6$

y,zの組み合わせは

（ⅱ）x=2の場合

$2x+y+z=8$に代入して

$4+y+z=8$

$y+z=4$

y,zの組み合わせは

（ⅲ）x=3の場合

$2x+y+z=8$に代入して

$6+y+z=8$

$y+z=2$

y,zの組み合わせは

 

したがって答えは5+3+1=9通り

 

まとめ