みなさんおはこんばんにちは。
ついつい汚れが気になると徹底的に掃除したくなるジルでございます！
今回は新たな三角形の面積の求め方をご教授します。
以前書いたこちらの記事で解いた問題を使ってみます。
$a=8,b=6,c=4$の三角形の面積は$S=3\sqrt{15}$でした。
その際、
①正弦定理・余弦定理を用いて、公式を使わずに解く方法
②$S=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C$を用いて解く方法
を紹介しました。
今回はまた違う解き方を勉強しましょう！
ヘロンの公式
早速公式紹介！
_____________________________________＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
この時
$s=\frac{a+b+c}{2}$
とおくと、三角形△ABCの面積Sは
$S=\sqrt{s(s-a)(s-b)(s-c)}$
で求められる。
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
こういうものです。
先程のa=8,b=6,c=4の三角形の面積をヘロンの公式を用いて求めてみましょう。
まずはsを求めましょう。
$s=\frac{8+6+4}{2}=9$
とまあ簡単に求められまして、次に本題の面積Sを求めます。
$S=\sqrt{9(9-8)(9-6)(9-4)}$
$=\sqrt{9 \times 1 \times 3 \times 5}=3\sqrt{15}$
練習問題（３通りの方法で解く）
ここ最近紹介した三角形の面積の求め方を確認しがてら問題を解いてみましょう！
問題：次のような△ABCの面積Sを求めなさい。a=3,b=6,c=7
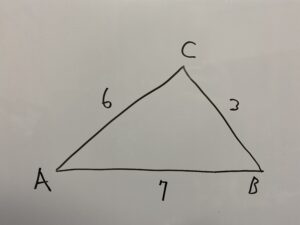
解①：正弦定理・余弦定理を使って解く
特別な公式を使わない場合はこの方法です。
今回の問題のように３辺の長さが出ている場合、次の手順で答えが出せます。
❷：❶で求めたcosを用いてsinを求める。
❸：❷で導いたsinを使って三角形の高さを求める。
❹：底辺×高さ×1/2で面積を出す。
❶：どこかの角のcosを求める。
B,Cそれぞれについて求めても結局最後は同じ答えになります。練習がてらやってみてください！
ではどうやって？みなさんもちろん分かりますね？そう『余弦定理』です！
❷：❶で求めたcosを用いてsinを求める。
こちらは
$\sin^2 θ + \cos^2 θ=1$
を使えばいけます。
$\sin^2 A +(\frac{19}{21})^2=1$
⇩（式変形）
$\sin^2 A=1-\frac{19^2}{21^2}=\frac{21^2-19^2}{21^2}$
ここで$21^2-19^2$の部分に注目。こちらの部分は展開して求めてもいいんですが、因数分解辺りで習った
$a^2-b^2=(a+b)(a-b)$
を使えば簡略化できます！
⇩（式変形）
$\sin^2 A=\frac{(21+19)(21-19)}{21^2}=\frac{40 \times 2}{21^2}=\frac{80}{21^2}$
⇩（式変形）
$\sin A=\frac{\sqrt{80}}{\sqrt{21^2}}$
⇩（式変形）←ちなみに三角形の性質上$0 \lt A \lt 180°＄より$\sin A \lt 0$
$\sin A=\frac{4\sqrt{5}}{21}$
❸：❷で導いたsinを使って三角形の高さを求める。
こちらの三角形に注目。
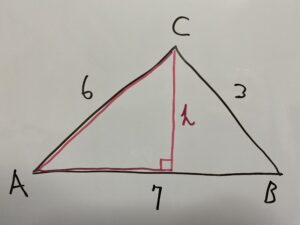
上の画像のように高さをと置くと
$\sin A=\frac{h}{6}$
よって❷で出したsinAを代入して
$\frac{4\sqrt{5}}{21}=\frac{h}{6}$
⇩（式変形）
$21h=24\sqrt{5}$
⇩（式変形）
$h=\frac{8\sqrt{5}}{7}$
❹：底辺×高さ×1/2で面積を出す。
ここまでこればあとは楽勝！
$S=7 \times \frac{8\sqrt{5}}{7} \times \frac{1}{2}=4\sqrt{5}$
解②：$S=\frac{1}{2}bc\sin A$を使って解く
次に公式を使ってみます。
❷：❶で求めたcosを用いてsinを求める。
❸：公式に代入する。
❶：どこかの角のcosを求める。
❷：❶で求めたcosを用いてsinを求める。
こちらは
$\sin^2 θ + \cos^2 θ=1$
を使えばいけます。
$\sin^2 A +(\frac{19}{21})^2=1$
⇩（式変形）
$\sin^2 A=1-\frac{19^2}{21^2}=\frac{21^2-19^2}{21^2}$
⇩（式変形）
$\sin^2 A=\frac{(21+19)(21-19)}{21^2}=\frac{40 \times 2}{21^2}=\frac{80}{21^2}$
⇩（式変形）
$\sin A=\frac{\sqrt{80}}{\sqrt{21^2}}$
⇩（式変形）←ちなみに三角形の性質上、$0° \lt A \lt 180°＄より$\sin A \lt 0 $
$\sin A=\frac{4\sqrt{5}}{21}$
❸：公式に代入する。
$S=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C$
に代入します。
今回はsinAが出ていますので、$S=\frac{1}{2}bc\sin A$を利用します。
$S=\frac{1}{2} \times 6 \times 7 \times \frac{4\sqrt{5}}{21}=4\sqrt{5}$
③：ヘロンの公式を使って解く
三辺の長さがそれぞれa,b,cの三角形△ABCを考える。
この時
$s=\frac{a+b+c}{2}$
とおくと、三角形△ABCの面積Sは
$S=\sqrt{s(s-a)(s-b)(s-c)}$
❷ヘロンの公式を使う。
❶sを求める。
$s=\frac{a+b+c}{2}$
に代入しましょう！
a=3,b=6,c=7より
$s=\frac{3+6+7}{2}=8$
❷ヘロンの公式を使う。
$S=\sqrt{s(s-a)(s-b)(s-c)}$にa=3,b=6,c=7,s=8を代入します。
$S=\sqrt{8(8-3)(8-6)(8-7)}$
$=\sqrt{8 \times 5 \times 2 \times 1}$
$=\sqrt{80}=4\sqrt{5}$
最後に（今回のまとめ）
３辺の長さが分かっている三角形の面積の求め方を３通り紹介しました。
❶：どこかの角のcosを求める。
❷：❶で求めたcosを用いてsinを求める。
❸：❷で導いたsinを使って三角形の高さを求める。
❹：底辺×高さ×1/2で面積を出す。
$\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C$を使って解く。
❶：どこかの角のcosを求める。
❷：❶で求めたcosを用いてsinを求める。
❸：公式に代入する。
❶sを求める。
❷ヘロンの公式を使う。
三辺の長さがそれぞれa,b,cの三角形△ABCを考える。
この時
$s=\frac{a+b+c}{2}$
とおくと、三角形△ABCの面積Sは
$S=\sqrt{s(s-a)(s-b)(s-c)}$
・公式を無理に覚えなくても解ける。
お、覚えきれねぇ…(-｡-;
大丈夫！私も公式はあまり覚えていません！笑
今回言いたかったことは、公式を無理に覚えなくてもやっていけるということ！
私は最低限のことしか覚えておりません。しかし大学数学科まで進学できました。
何度も言っていますが、大事なのは場数です。
たくさん問題を解きましょう。繰り返しときましょう。
それが一番の近道です。
楽しい数学Lifeを！
