
みなさんおはこんばんにちは。
Apex全然上手くならなくてぴえんなジルでございます!
今回は三角比において大変重要で便利な定理を紹介します!
『正弦定理』、『余弦定理』
になります。
正弦定理
まずはこちら正弦定理になります。
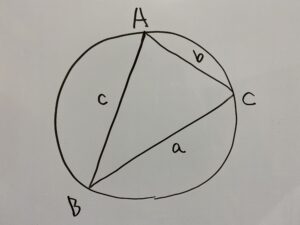
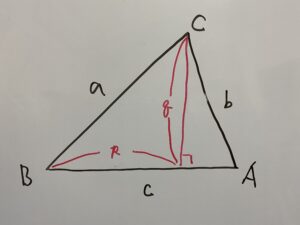
次のような円において、その半径をRとすると

下に証明を書いておきます。
定理を覚えれば問題ありませんが、なぜ正弦定理が成り立つのか気になる方はご覧ください!
余弦定理
次はこちら余弦定理です。
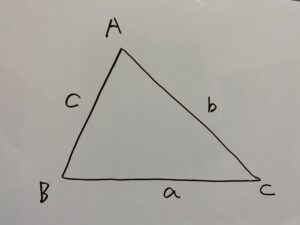
において
が成立します。

こちらも下に証明を載せておくので興味のある方はぜひご覧ください!
余弦定理から分かること
が成立しますね。またa,b,cは辺なため、正の数です。
つまり
が成立するわけですよ。
そして
と言います。以上のことから次の法則が成り立ちます。

において
Aが鋭角 ⇔
Aが直角 ⇔
Aが鈍角 ⇔
正弦定理の証明
Aが鋭角か鈍角かで分けます。
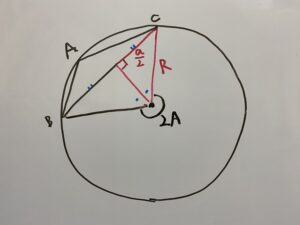
Aが鋭角の場合
こちらの外接円を用いて説明します。
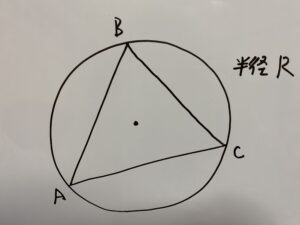
こちらの三角形に注目しましょう。
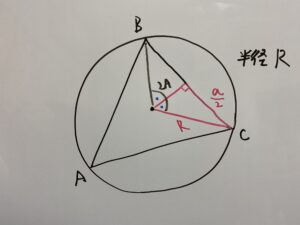
θについて、三角形の内角の合計が180°なので
また
⇩(両辺×2)
⇩(式変形)
⇩(θ=90°-A)
⇩(
これで証明完了です。
Aが鈍角の場合
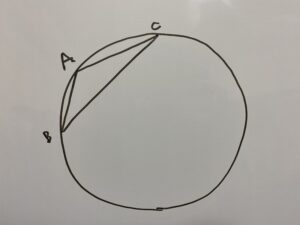
こちらを使います。
次のような三角形を考えます。
また三角形の内角の和が180°より
よって
ここで
つまり
⇩(両辺×R)
⇩(両辺×2)
⇩(両辺÷
余弦定理の証明
次は余弦定理の証明です。
Aが鋭角の場合
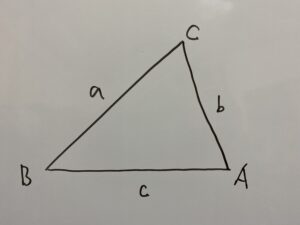
この三角形を使って証明します。
まずは1本の線を引きます。
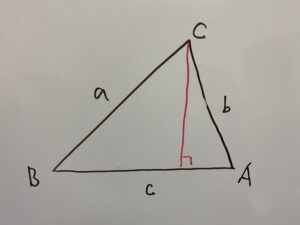
そして2本の辺を定義します。
三平方の定理より
p,qについて
代入して
⇩(展開)
⇩(カッコで括る)
⇩(
Aが鈍角の場合
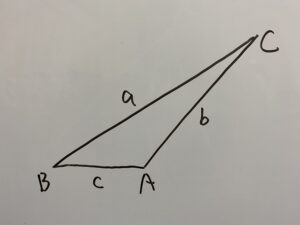
この三角形を使って証明します。
まずは線を付け加えて準備します。
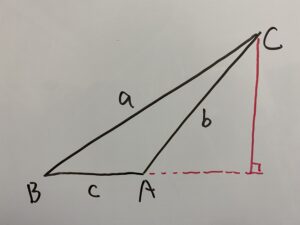
そしてp,qを定義します。
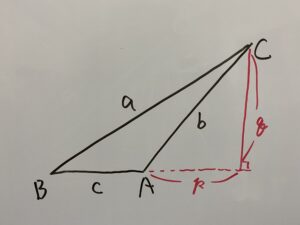
三平方の定理より
p,qについて
⇩(bを移項)
ここで、
これらを代入して
⇩(展開)
⇩(カッコで括る)
⇩(
最後に
今回紹介した定理は必ず覚えてください。
この分野では必須の定理です。
次はこの定理を利用する問題を解説したいと思います。

楽しい数学Lifeを!



