
みなさんおはこんばんにちは。
寒すぎて冬眠しそうなジルでございます!
今回は三角比の拡張についての練習問題をいくつか用意しました!
次の不等式を解きなさい。
今回は
この問題を解くには
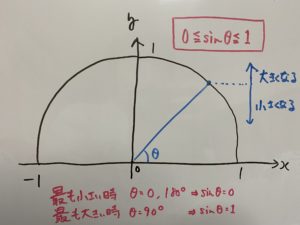
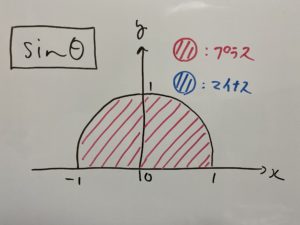
____________________________________________________________________________________
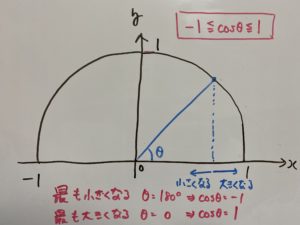
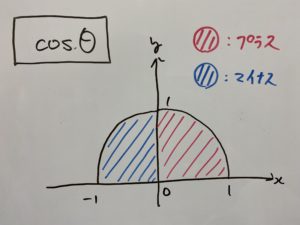
____________________________________________________________________________________
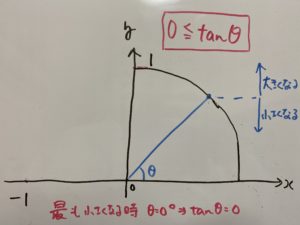
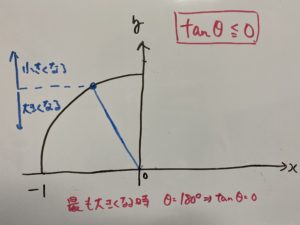
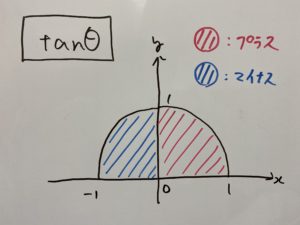
____________________________________________________________________________________
この知識が必要になります。
この辺り忘れた方へ、こちらの記事をぷれぜんとふぉーゆー

(1)
ここでこのパターンの問題の解き方手順を書き記します。
②簡単な図を書く。 ←慣れれば省略してもオッケー
大抵これで大丈夫です(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
今回出題した問題は全てこれを使って解きます。
①
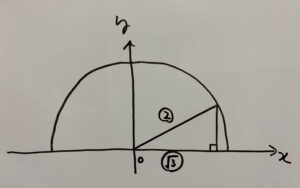
この三角形パターンなので、

三平方の定理にて出てくる定番の三角形ですね?忘れてないですか?必ず覚えてください!
②

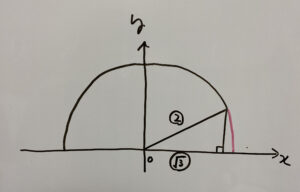
したがって
(2)
①
この2箇所ですね?
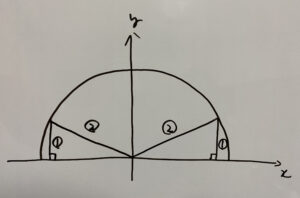
したがって
②

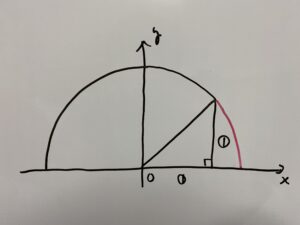
よって次の赤色部分です。
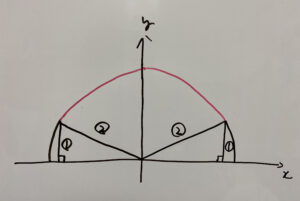
つまり
(3)
①
これは次のパターンになります。
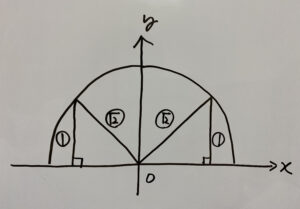
したがって

先ほどと同じく、三平方の定理で頻出した三角形ですね。
②

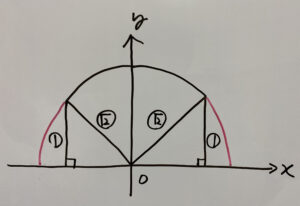
したがって

この解答を見ると
この辺りはしっかり意識しましょう。
(4)
①
これを満たす三角形は
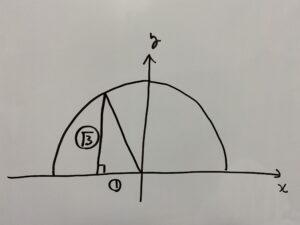
です。よって
これを満たす三角形は
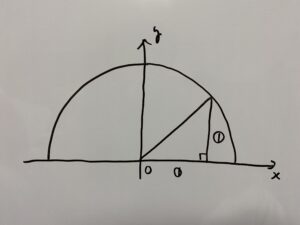
です。よって
②
①で出した
$\tan θ (90° \lt θ \leqq 180°)は次のように変化します。

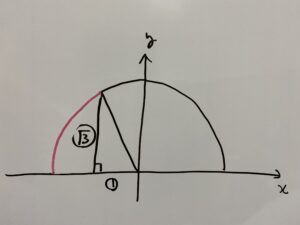
したがって
$\tan θ (0° \lt θ \leqq 90°)は次のように変化します。

したがって
以上のことから答えは
最後に
しっかり図を書いて解くと理解しやすいかと思います。
めんどくさいかもですが図は書いたほうがいいです。

楽しい数学Lifeを!



