みなさんおはこんばんにちは、ジルでございます！
前回に引き続き『二次関数』を取り上げます。
今回は平行移動について解説します。
まず始めに（確認事項）
平行移動を学ぶには軸・頂点の求め方を知っている必要があります。
前回その記事を書きましたので不安な方はご確認ください。
今回はその辺りの知識を知っている前提でお話ししていきます。
文字を使って説明してみる。
まずは手順を文字を使って説明してみます。
あとで練習問題やるよ！
$y=a(x-p)^2+q$の形に変形する
これは前回の軸・頂点の記事で学習しましたね？
まだよく分かっていない方は上に貼った記事を見返してみてね！
さてこの式を平行移動させてみましょう！
$y=a(x-p)^2+q$を$x$軸方向に$j$、$y$軸方向に$k$平行移動した時
まずは文字を用いてみます。
ちなみに「$x$軸方向」、「$y$軸方向」とは
『$x$軸のプラスの方向（右方向）』、『$y$軸のプラスの方向（上方向）』
ということです。
ここで一つ大事なこと言います。
平行移動するとは、
”グラフの形はそのままで”移動するということです。
つまりですよ？
『頂点をいじりさえすればいい』
ということです。
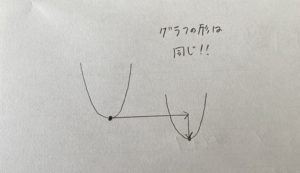
では式に表してみましょう。
$y=a(x-p)^2+q$の頂点は$(p,q)$ですね？
この頂点を$x$軸方向に$j$、$y$軸方向に$k$平行移動させるとどうなるか？
ズバリ$(p+j,q+k)$です！
分かりますか？
例えば$(2,3)$を$x$軸方向に$-3$、$y$軸方向に$1$移動させると
$(2+(-3),3+1)$すなわち$(-1,4)$になります。
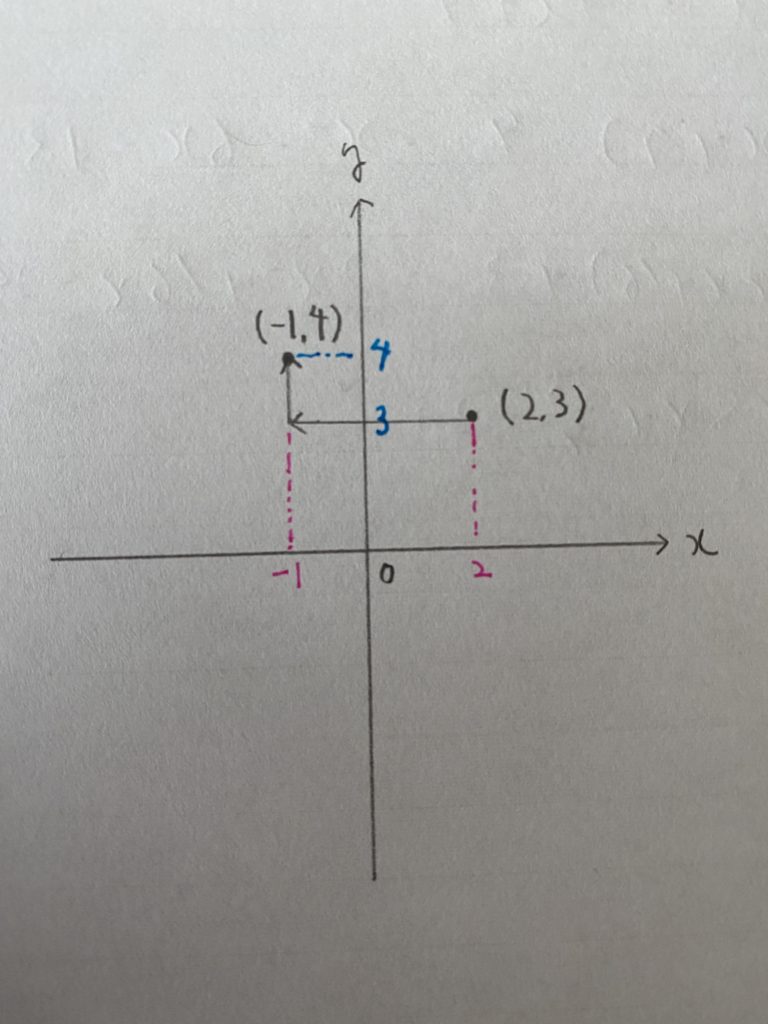
ここで核心にせまります。
文字ばっかりで大変ですが頑張ってついてきてください！
あとで具体的に問題やってみるのでそれも併せて見てもらえば理解が深まると思います。
グラフの形は
$y=a(x-p)^2+q$
と同じで、頂点が
$(p+j,q+k)$
な訳ですから、ズバリ式は
$y=a\{x-(p+j)\}+(q+k)$
となります。
これは理解しておいてください。したらこの公式がすぐ頭に浮かぶようになりますよ！
$$y=a\{x-(p+j)\}^2+(q+k)$$
具体的に問題を解いてみよう！
やはり数学が上達するには問題をたくさん解くのが一番！
早速１問解いてみましょう！
$y=2x^2-4x+1$を$x$方向に$-4$、$y$方向に$-3$平行移動してみよう！
こちらの問題。
できるだけ丁寧に解説しますのでついてきてください。
$y=a(x-p)^2+q$の形にする。
①$x^2$の項と$x$の項をカッコで括る。
$y=(2x^2-4x)+1$
②$x^2$の係数をカッコの外に出す。
$y=2(x^2-2x)+1$
③$y=a(x-p)^2+q$の形に持っていく。
$y=2\{(x^2-2x+1)-1\}+1=2(x-1)^2-2+1=2(x-1)^2-1$
よって軸：$x=1$ 頂点：$(1,-1)$
平行移動させる。
先ほど表した公式をもう一度書きます。
$y=a(x-p)^2+q$を$x$軸方向に$j$、$y$軸方向に$k$平行移動させると
$$y=a\{x-(p+j)\}^2+(q+k)$$
これを使います。
$y=2\{x-(1-4)\}^2-1-3=2(x+3)^2-4$
解けました！ 答え $y=2(x+3)^2-4$
最後にまとめ
今回の記事をまとめます。
①$y=a(x-p)^2+q$の形を作る。
②$y=a\{x-(p+j)\}^2+(q+k)$
楽しい数学Lifeを！
