みなさんおはこんばんにちは、ジルでございます！
前回は二次関数の「最大値・最小値」の求め方の基礎を勉強しました。
今回はもう少し掘り下げてみたいと思います。
$y=ax^2+bx+c$の最大値・最小値を求めてみよう！
前回は簡単な二次関数の最大値・最小値を求めました。
今回はもう少し難しめの二次関数でやってみましょう！
解き方
簡単に手順をまとめます。
❶$y=a(x-p)^2+q$の形に持っていく。
❷与えられた定義域が頂点を含んでいるかどうかを確認する。
❸のⅰ与えられた定義域が頂点を含んでいる場合。
❸のⅱ与えられた定義域が頂点を含んでいない場合。
こんな感じです。
それぞれ解説していきます。
$y=a(x-p)^2+q$の形に持っていく。
まずはこれ。
あれ？やり方忘れたぞ？のために改めて記事貼っときます( ^ω^ )
与えられた定義域が頂点を含んでいるかどうかを確認する。
こちらを確認しましょう。
含んでいるかどうかで少し状況が変わります。
ⅰ与えられた定義域が頂点を含んでいる場合。
この場合は
最大値あるいは最小値が頂点になります。
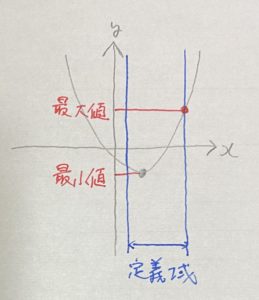
この場合頂点が最小値になります。
問題は最大値の方です。
注目すべきは
定義域の左端と右端の$x$座標と頂点の$x$座標との距離
です。
先ほどの二次関数を見てください。
分かりますか？定義域の左端と右端、それぞれと頂点の$x$座標との距離を比べて、遠い方が最大値なんですね実は！
頂点の$y$座標が最小値
定義域の左端と右端、それぞれと頂点の$x$座標との距離で遠い方が最大値
次に
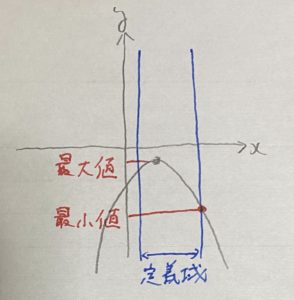
こちらを見てみましょう。今回は頂点が定義域に入っている場合です。
先ほどの逆山形の場合を参考にすると
頂点の$y$座標が最大値
定義域の左端と右端、それぞれと頂点の$x$座標との距離で遠い方が最小値
になります。
ⅱ与えられた定義域が頂点を含んでいない場合。
この場合は頂点は最大値にも最小値にもなりません。
注目すべきは定義域の左端と右端です。
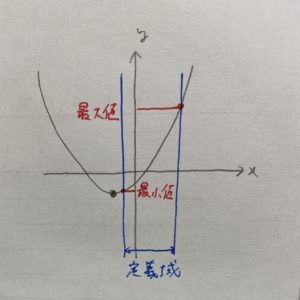
この場合は
最小値 定義域左端の二次関数の$y$座標
最大値 定義域右端の二次関数の$y$座標
となることがグラフから分かるかと思います。
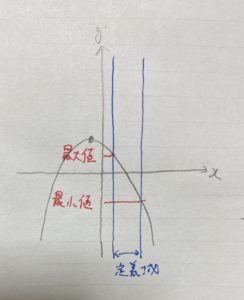
この場合は
最小値 定義域右端の二次関数の$y$座標
最大値 定義域左端の二次関数の$y$座標
となります。
文章で表してみると、要は
$y=a(x-p)^2+q$において
$a \gt 0$の時
最小値は「定義域の左端と右端のうち、頂点に近い方」
最大値は「定義域の左端と右端のうち、頂点に遠い方」
$a \lt 0$の時
最小値は「定義域の左端と右端のうち、頂点に遠い方」
最大値は「定義域の左端と右端のうち、頂点に近い方」
になります！
たくさん問題を解いて理解してください。
文章だけを覚えても対して力になりません。
数学のブログで何度も口酸っぱく言っていますが、
「たくさん問題を解くことが数学上達の近道！努力は裏切らない！」
実際に問題を解いてみよう！
一通り説明したので後は実際に解くのみ！
もちろん解説も書いておきますが分からなかったら、以前の記事、上で書いた解説を何度も見返してみましょう！
では早速やってこう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
$y=x^2-6x+14$ $( 4 \leqq x \leqq 6)$
まずはこちらの問題の最大値・最小値を求めましょう。
❶$y=a(x-p)^2+q$に式変形する。
$y=x^2-6x+14=(x^2-6x)+14=\{(x^2-6x+9)-9\}+14=(x^2-6x+9)+5$
$=(x-3)^2+5$
これで頂点が$(3,5)$であることが分かりました。
❷頂点が定義域に入っているか確認する。
今回の定義域は$4 \leqq x \leqq 6$で、頂点は$(3,5)$。
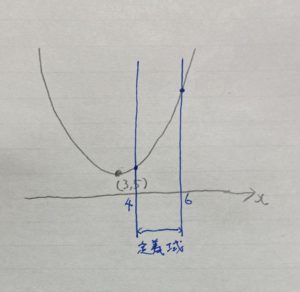
入っていませんね？なので先ほどの「❸のⅱ」を参考にします。
❸のⅱ
先ほどの画像を見てください。
$x=4$の時の$y$の値が最小値、$x=6$の時の$y$の値が最大値をとります。
$x=4$の時
$y=4^2-6 \times 4+14=6$
$x=6$の時
$y=6^2-6 \times 6+14=14$
答え 最小値 6 最大値 14
$y=-2x^2+8x-7$ $(0 \leqq x \leqq 3)$
次にこちらの最小値・最大値を求めましょう。
❶$y=a(x-p)^2+q$に式変形する。
$y=(-2x^2+8x)-7=-2(x^2-4x)-7=-2\{(x^2-4x+4)-4\}-7$
$=-2(x^2-4x+4)+8-7=-2(x-2)^2+1$
これで頂点が$(2,1)$であることが分かりました。
❷頂点が定義域に入っているか確認する。
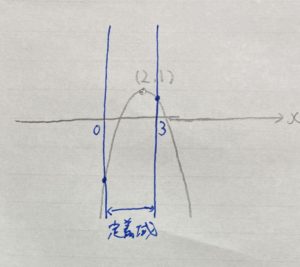
入っています。なので先ほどの「❸のⅰ」を参考にします。
❸のⅰ
さきほどの画像を見てみましょう。
最大値が頂点であることが分かりますね？
問題は最小値です。
頂点の$x$座標は2です。そして今回の定義域の左端は0、右端は3。
２から遠いのは勿論「０」です。よって最大値は$x=0$の時の$y$の値です。
$x=0$の時の$y$の値は
$y=-2 \times 0^2+8 \times 0-7=-7$
答え 最小値 -7 最大値 1
最後に
今回は二次関数の最小値・最大値についての一般基礎クラスの問題を解説しました。
次回は応用問題を解説します。お楽しみに！
楽しい数学Lifeを！
